Question

A girl 5.5feet cast a shadow 70inch long. At the same time telephone post cast a shadow 314inch long. Which proportion cannot be used to find the height of a telephone pole?
A. \[\left( \dfrac{70}{5.5} \right)=\left( \dfrac{314}{x} \right)\]
B. \[\left( \dfrac{70}{314} \right)=\left( \dfrac{5.5}{x} \right)\]
C. \[\left( \dfrac{x}{5.5} \right)=\left( \dfrac{314}{70} \right)\]
D. \[\left( \dfrac{70}{x} \right)=\left( \dfrac{5.5}{314} \right)\]

Answer 1

Hint: The shadow of the girl and pole cast at the same time so the leaning angle of both shadows will be the same. So we can use the formulae \[\tan \alpha =\dfrac{height}{base}\] to find the leaning angle. Put the value in the question and evaluate it to find the value. After finding the leaning angel we can use it to find the height of the telephone pole by calculating the rest of the problem. And cancel out the right option in the question.

Complete step by step answer:
According to the question, the height of a girl is 70inch when the height of the shadow of telephone pole is 314inch.
We can understand from this that the height of the sun is the same when both the shadows are measured. So that the leaning angel of the shadow is also the same.
Let the leaning angle be \[\alpha \].

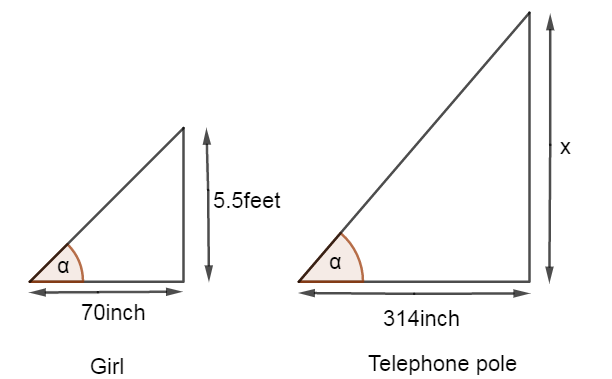
Here in the diagram we can clearly see that the leaning angle of the shadow is \[\alpha \].
The height of the girl is 5.5 feet.
We know the base and height and leaning angle of a triangle. Hence we can use the formulae\[\tan \alpha =\dfrac{height}{base}\]. By putting the value of base=70inch and height=5.5feet we can find the leaning angle of the shadow of the girl.
\[\tan \alpha =\dfrac{5.5}{70}\]
So the leaning angle of the shadow is \[\tan \alpha =\dfrac{5.5}{70}\]
According to the question the girl casts a shadow at the same time when the telephone pole casts a shadow. So the leaning angle of the shadow of the girl and the telephone pole is the same.
Let us assume the height of the telephone pole is x.

Now,
\[\tan \alpha =\dfrac{x}{314}\]
Putting the value of \[\tan \alpha \] we get,
\[\dfrac{5.5}{70}=\dfrac{x}{314}\]
Now we can change the variable to make the equation look like the option is given in the question.
\[\Rightarrow \left( \dfrac{70}{5.5} \right)=\left( \dfrac{314}{x} \right)\] (Option A)
\[\Rightarrow \left( \dfrac{70}{314} \right)=\left( \dfrac{5.5}{x} \right)\] (Option B)
\[\Rightarrow \left( \dfrac{x}{5.5} \right)=\left( \dfrac{314}{70} \right)\] (Option C)
But it is impossible to make Option D with this equation. So we can conclude that proportion \[\left( \dfrac{70}{x} \right)=\left( \dfrac{5.5}{314} \right)\] cannot be used to find the height of a telephone pole.

Note:
Students have to understand the leaning angle of the shadow. They took the right angle \[\left( {{90}^{\circ }} \right)\] as a leaning angle and then the calculation went horribly wrong. Students has to remember the value of \[\tan \alpha \] which is \[\tan \alpha =\dfrac{height}{base}\] if you write it as \[\tan \alpha =\dfrac{base}{height}\] you will get this math problem wrong.