Question

A girl 5.5 feet cast a shadow 70 inches long. At the same time a telephone pole casts a shadow 314 inches long. Which proportion cannot be used to find the length of the telephonic pole?
(A) \[\left( {\dfrac{{70}}{{5.5}}} \right) = \left( {\dfrac{{314}}{x}} \right)\]
(B) \[\left( {\dfrac{{70}}{{314}}} \right) = \left( {\dfrac{{5.5}}{x}} \right)\]
(C) \[\left( {\dfrac{x}{{5.5}}} \right) = \left( {\dfrac{{314}}{{70}}} \right)\]
(D) \[\left( {\dfrac{{70}}{x}} \right) = \left( {\dfrac{{5.5}}{{314}}} \right)\]

Answer 1

Hint:
At the same time, the position of the sun will remain the same for both girl and telephonic pole. Resulting in subtending the same angle by the shadow’s of both.
Using formula we can solve this question: \[\tan \theta = \dfrac{{Perpendicular}}{{Base}} = \dfrac{{length{\text{ }}of{\text{ }}the{\text{ }}observer}}{{length{\text{ }}of{\text{ }}the{\text{ }}shadow{\text{ }}of{\text{ }}the{\text{ }}observer}}\]

Complete step by step solution:

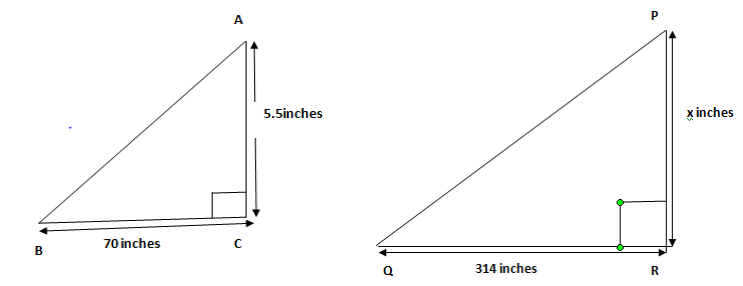
 Let the height of the telephonic pole be x inches.
Given: Height of the girl=5.5 inches
             Length of the shadow of the girl=70 inches
\[In{\text{ }}\Delta ABC;\]
\[ \Rightarrow \tan \angle ABC = \dfrac{{AC}}{{BC}} = \dfrac{{5.5}}{{70}}\]
Height of the telephonic pole=x inches inches.
 Length of the shadow of the girl=70 inches.
\[In{\text{ }}\Delta PQR;\]
\[ \Rightarrow \tan \angle PQR = \dfrac{{PR}}{{QR}} = \dfrac{x}{{314}}\]
Since, these two conditions are following at the same time so the position of the sun will be fixed for both resulting in subtending the same angle.
\[ \Rightarrow \tan \angle ABC = \tan \angle PQR\]
\[ \Rightarrow \dfrac{{5.5}}{{70}} = \dfrac{x}{{314}}\]
Clearly, the proportions used in Option (D) is incorrect.

Option (D) is the correct answer.

Note:
In this question, we will compare the proportions as angle subtending by both observers will be the same. Trigonometric ratios are helpful in solving such questions because these are also rations but it is connected with the subtended angle also. which makes it special.