Question

A geostationary satellite is a height h above the surface of earth. If earth radius R
(A) The minimum colatitudes on earth up to which the satellite can be used for communication is $ \text{Si}{{\text{n}}^{-1}}\left( \text{R}/\text{R}+\text{h} \right) $ .
(B) The maximum colatitudes on earth up to which the satellite can be used for communication is $ \text{Si}{{\text{n}}^{-1}}\left( \text{R}/\text{R}+\text{h} \right) $
(C) The area on earth escaped from this satellite is given as $ 2\text{ }\!\!\pi\!\!\text{ }{{\text{R}}^{2}}\left( 1+\sin \text{ }\!\!\theta\!\!\text{ } \right) $
(D) The area on earth escaped from this satellite is given as $ 2\text{ }\!\!\pi\!\!\text{ }{{\text{R}}^{2}}\left( 1+\cos \text{ }\!\!\theta\!\!\text{ } \right) $

Answer 1

Hint: A satellite which appears to be at a fixed position at a definite height (i.e., stationary) to an observer on earth is called a geostationary satellite. This satellite is also called a geosynchronous satellite as its angular speed is synchronized with the angular speed of the earth about its axis, i.e. this satellite revolves around the earth with same angular speed in the same direction as is done by earth around its axis.
To calculate the height of geostationary satellite, we use
 $ h={{\left( \dfrac{{{T}^{2}}{{R}^{2}}g}{4{{\pi }^{2}}} \right)}^{\dfrac{1}{3}}}-R $
Co-latitudes means the difference between a given latitude and $ {{90}^{{}^\circ }} $ . Co-latitude of any position on earth is the angle the line from centre of the earth to the position forms with the axis of rotation of earth.

Complete step by step solution
Consider that B is the position of the geostationary satellite.

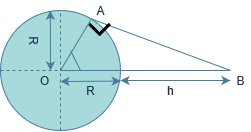
In the given figure,
 $ \theta $ Is the latitude and $ \phi $ is the co-latitude of a place which can directly receive a signal from a geostationary satellite.
In triangle OAB, we have:
 $ \cos \phi =\dfrac{R}{R+h} $
That is $ \phi ={{\cos }^{-1}}\dfrac{R}{R+h} $
Now, $ \theta =\dfrac{\pi }{2}-\phi $
 $ \therefore \theta =\dfrac{\pi }{2}-{{\cos }^{-1}}\dfrac{R}{R+h} $
 $ \theta ={{\sin }^{-1}}\dfrac{R}{R+h} $
So, this is the minimum Co-latitude on earth up to which the satellite can be used for communication.
Now we will find out the area on the earth escaped from this satellite.
Infinitesimal area on sphere is given by $ dA={{R}^{2}}\sin \theta d\theta d\phi $ ( $ \theta $ is the latitude of place)
Therefore the area of the reach of the satellite is
 $ \int_{0}^{A}{dA=\int\limits_{0}^{2\pi }{\int\limits_{0}^{\theta }{{{R}^{2}}}\sin \theta d\theta d\phi }} $
Hence $ A=2\pi {{R}^{2}}\left( 1-\sin \theta \right) $
Area on earth escaped from satellite= $ 4\pi {{R}^{2}}-A $
= $ 4\pi {{R}^{2}}-2\pi {{R}^{2}}\left( 1-\sin \theta \right) $
= $ 2\pi {{R}^{2}}\left( 1+\sin \theta \right) $
Therefore, this is the area on earth that escaped from this satellite.
Hence option (A) and (C) is correct.

Note
Remember some rule of trigonometry and integration. Integration and trigonometry plays an important role in physics. There are some essential conditions for this satellite:
A geostationary satellite should be at a height nearly 3600 km above the equator of earth.
Its period of revolution around the earth should be the same as that of earth about its axis, i.e., exactly 24 hours.
It should revolve in an orbit concentric and coplanar with the equatorial plane, so the plane of the orbit of the satellite is normal to the axis of rotation of the earth.
Its sense of rotation should be the same as that of the earth about its own axis, i.e., from west to east. Its orbital speed is nearly $ 3\cdot 1km/s $ .