Question

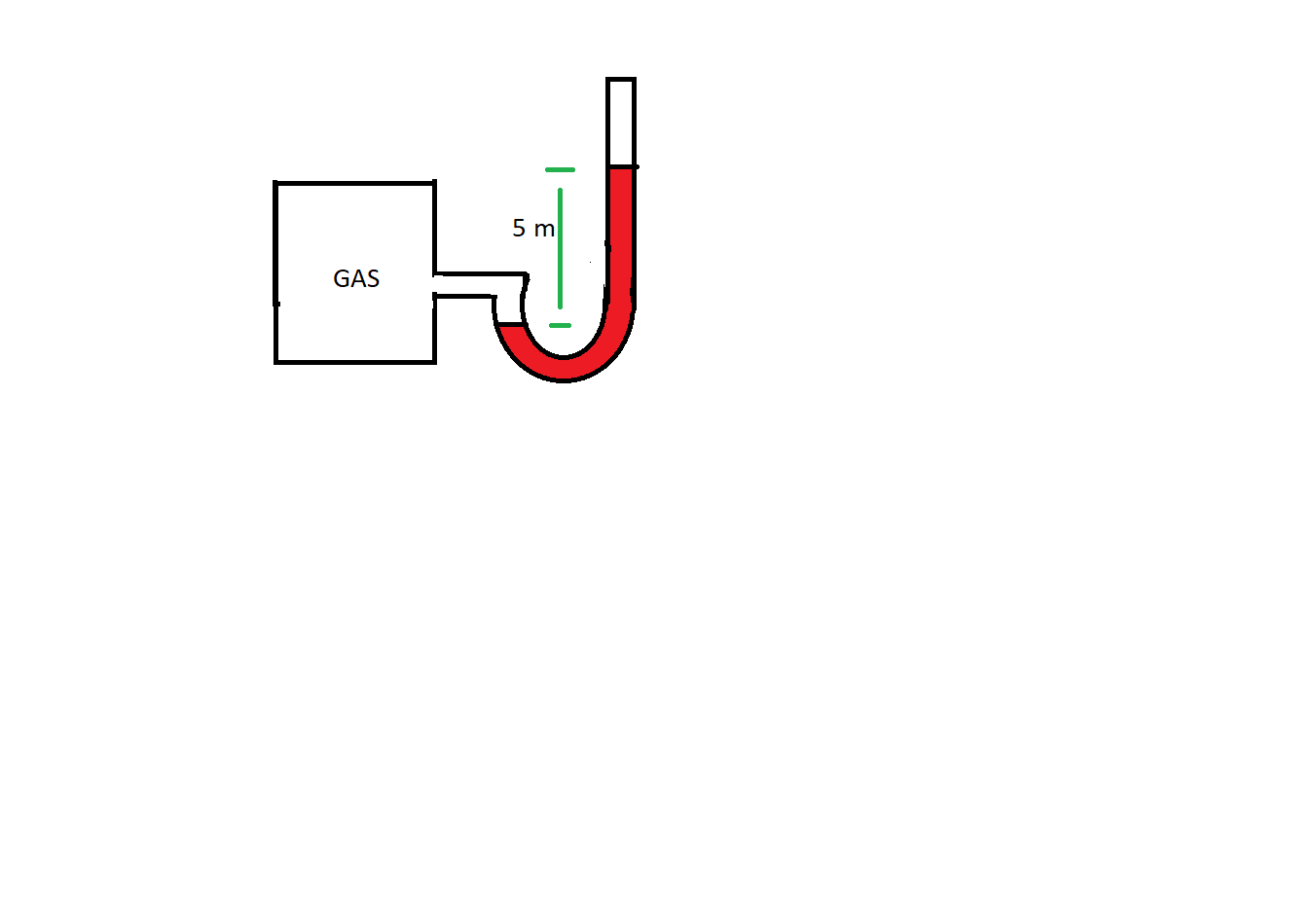
A gas jar of 10-liter volume filled with ${ O }_{ 2 }$ at 300 K is connected to the glycerine manometer. The manometer shows a 5 m difference in the level as shown in the figure. What will be the number of moles of ${ O }_{ 2 }$ in the gas jar?
(${ d }_{ glycerin }$ = 2.72 g/ml; ${ d }_{ mercury }$ = 13.6 g/ml)

Answer 1

Hint: You have to use this relation first: $h_{ (Hg) }\rho _{ (Hg) }g=h_{ (gly) }\rho _{ (gly) }g$. Then use the ideal gas equation to get the final answer, moles of oxygen.


Complete step by step solution:
Let’s calculate the number of moles of oxygen.
We have the following data -
Volume of container = 10 Liter
Temperature = 300 K
Density of glycerine = 2.72 g/mL
Density of mercury = 13.6 g/mL
Height difference by glycerine = 5 m
First, we have to calculate the height of mercury.
The formula used: $P=h\rho g$

where,
P is pressure, h is height, g is the acceleration due to gravity, and $\rho$ is density.
The expression for glycerine and mercury will be:
${ P }_{ (Hg) }=h_{ (Hg) }\rho _{ (Hg) }g$
${ P }_{ (gly) }=h_{ (gly) }\rho _{ (gly) }g$
Now, we can write,
$h_{ (Hg) }\rho _{ (Hg) }g=h_{ (gly) }\rho _{ (gly) }g$
$h_{ (Hg) }\rho _{ (Hg) }=h_{ (gly) }\rho _{ (gly) }$
Now put all the given values in this expression, we get:
$h_{ (Hg) }\times (13.6g/mL)=(5m)\times (2.72g/mL)$
$h_{ (Hg) }=1m$
Now we have to calculate the pressure of the gas.
$P_{ gas }=0.76dg+1dg=1.76dg=1760mmHg$
(1 atm = 760 mmHg)
$1760mmHg=\frac { 1760 }{ 760 } atm$
Now we have to calculate the moles of gas.
Using ideal gas equation:
PV = nRT
where,
P = Pressure of gas = $\frac { 1760 }{ 760 } atm$
V = Volume of gas = 10 L
n = number of moles of gas = ?
R = Gas constant = 0.0821 L.atm/mol.K
T = Temperature of gas = 300 K
Putting values in the above equation, we get:
$(\frac { 1760 }{ 760 } atm)\times 10L=n\times (0.0821L.atm/mol.K)\times 300K$
$n=\frac { 94 }{ 100 } =0.94mole$

Therefore, we can conclude that the moles of ${ O }_{ 2 }$ in the gas jar will be 0.94 mol.

Note: We should know that a manometer is a device that measures air pressure using a container with a "U"-shaped tube open at one or both ends.
In the manometer, The height of the fluid on the open side will be higher on that side when air pressure is less than the gas pressure and lower on the open side when the air pressure exceeds the gas pressure.