Question

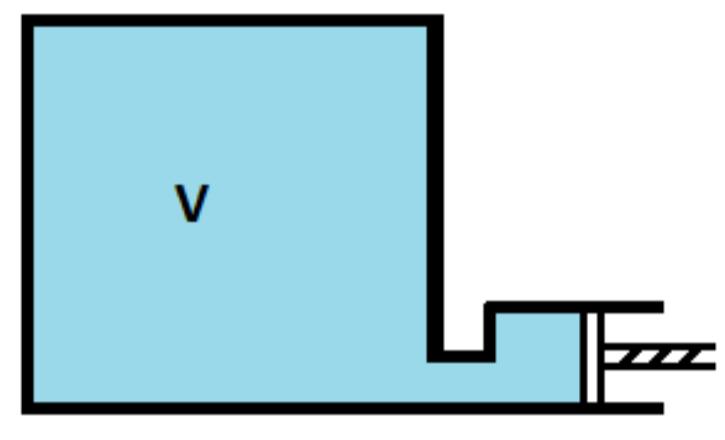
A gas is enclosed in a vessel of volume V at a pressure P. It is being pumped out of the vessel by means of a piston pump with a stroke volume $\dfrac{\text{V}}{100}$. What is the final pressure in the vessel after n strokes of the pump? Assume no change in temperature during pumping out of gas.

Answer 1

Hint: We have a vessel with gas-filled inside it. The gas is pumped out using a piston pipe and the stroke volume is given to us. We have the ideal gas equation and the equation at a constant temperature. Since the process given here is an isothermal condition we can use the equation at constant temperature and find the pressure for all strokes.
Formula used:
Ideal gas equation,
$PV=nRT$
For constant temperature,
${{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$

Complete step-by-step solution:
We have a gas in a vessel with volume ‘V’.
The pressure in the vessel is given as ‘P’.
Now, this gas is pumped out of the vessel using a piston pump.
And the stroke volume is given as $\dfrac{\text{V}}{100}$ .
It is said that we are performing “n” number of strokes.
We have the ideal gas equation,
 $PV=nRT$, was ‘T’ is temperature, ‘R’ is the gas constant, ‘n’ is the total number of moles, ‘V’ is the volume, and ‘P’ is pressure.
Here it is said that we have an isothermal situation, i.e. there is no change of temperature during the pumping out of gas.
Now, let us consider the first stroke.
After the first stroke, the pressure will become ${{P}_{1}}$ and the volume will become ${{V}_{1}}$
We know at constant temperature,
$PV={{P}_{1}}{{V}_{1}}$
After one stroke, the volume will become,
${{V}_{1}}=V-\dfrac{V}{100}$
Therefore we can say that,
$PV={{P}_{1}}\left( V-\dfrac{V}{100} \right)$
Then the pressure after one stroke will become,
$\begin{align}
  &\Rightarrow {{P}_{1}}=P\left( \dfrac{V}{V-\dfrac{V}{100}} \right) \\
 &\Rightarrow {{P}_{1}}=P\left( \dfrac{100}{99} \right) \\
\end{align}$
When the gas is pumped for the second time, the pressure will become ${{P}_{2}}$ and volume will become ${{V}_{2}}$
Hence we can say that.
${{P}_{1}}{{V}_{1}}={{P}_{2}}{{V}_{2}}$
We know that after the first stroke the mass of the gas will decrease, But the volume of the container will remain unchanged hence the volume of the gas also remains the same.
Therefore the volume before the second stroke will still be ‘V’; i.e. we can take and the volume ${{V}_{1}}$ as V.
And the volume after the second stroke will become,
${{V}_{2}}=V-\dfrac{V}{100}$
Hence,
${{P}_{1}}V={{P}_{2}}{{V}_{2}}$
$\Rightarrow{{P}_{1}}V={{P}_{2}}\left( V-\dfrac{V}{100} \right)$
Therefore we get ${{P}_{2}}$ as,
$\begin{align}
  &\Rightarrow {{P}_{2}}={{P}_{1}}\left( \dfrac{V}{V-\dfrac{V}{100}} \right) \\
 &\Rightarrow {{P}_{2}}={{P}_{1}}\left( \dfrac{100}{99} \right) \\
 &\Rightarrow {{P}_{2}}=P{{\left( \dfrac{100}{99} \right)}^{2}} \\
\end{align}$
Similarly, we get the pressure in the vessel after ‘n’ strokes as,
${{P}_{n}}=P{{\left( \dfrac{100}{99} \right)}^{n}}$

Note: The volume of the gas in the vessel is given. Consider “m” is the initial mass of the gas inside the vessel. After the first stroke, the mass of the gas will decrease to ${{m}_{1}}$, and with each stroke, the mass will continue to decrease. But the vessel remains the same, and hence the volume of the vessel also remains the same.
Therefore the remaining mass of the gas will fill the volume of the vessel. Thus the volume of the gas remains constant.