Question

A gas cylinder has a diameter of 14m and height is 0.2m. Find its surface area. \[\left( \pi =\dfrac{22}{7} \right)\].
A. 316.512 \[m{{m}^{2}}\]
B. 316.512 \[m\]
C. 316.512 \[{{m}^{3}}\]
D. 316.512 \[{{m}^{2}}\]

Answer 1

Hint: Firstly we have to draw a clear diagram to understand the problem properly. Now we have to calculate radius from diameter by the formulae \[r=\dfrac{R}{2}\] where “r” is radius and “R” is the diameter of the gas cylinder. Then we have to find total surface area by adding curved surface area and base surface area. Curved surface area is the product of circumference of circle and height of cylinder, whereas base surface area is the area of circles on top and bottom. After getting the total surface area formulae we have to put the values given in the question and calculate.

Complete step by step solution:
The diameter of the gas cylinder is 14m. We can calculate the radius from diameter.
\[r=\dfrac{R}{2}\] where “r” is radius and “R” is the diameter of the gas cylinder.
Now putting the value of “R” we get,
\[\begin{align}
  & r=\dfrac{14}{2} \\
 & \Rightarrow r=7 \\
\end{align}\]
The radius of the gas cylinder is 7m.

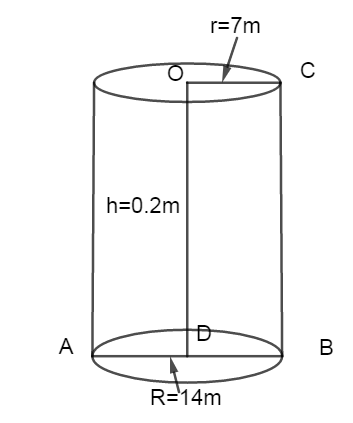
In the diagram we can clearly see the radius, diameter and the height of the gas cylinder.
Now we have to find the surface area of the cylinder. To find the surface area we have to find the curved surface area and the base surface area.
The curved surface area of a cylinder (CSA) is defined as the area of the curved surface of any given cylinder having base radius ‘r’, and height ‘h’, It is also termed as Lateral surface area (LSA). The formula for a curved area or lateral area is
\[CSA=2\times \pi \times r\times h\text{ square units}\]
And the base of the cylinder is in a circular shape. Hence, by the formula of area of the circle, we know, Area of the circular bases of the cylinder is \[2\left( \pi {{r}^{2}} \right)\] as the cylinder has two circular bases.
The total surface area of a cylinder is equal to the sum of areas of all its faces. The Total surface area with radius ‘r’, and height ‘h’ is equal to the sum of the curved area and circular areas of the cylinder is
\[\begin{align}
  & 2\times \pi \times r\times h+2\times \pi \times {{r}^{2}} \\
 & \Rightarrow 2\pi r\left( h+r \right)\text{ square units} \\
\end{align}\]
Now putting the value of \[\pi \], r and h we get,
\[\begin{align}
  & \Rightarrow 2\times \dfrac{22}{7}\times 7\times \left( 0.2+7 \right) \\
 & \Rightarrow 44\times 7.2 \\
 & \Rightarrow 316.8 \\
 & \approx 316.512 \\
\end{align}\]

The surface area of the gas cylinder is 316.512 \[{{m}^{2}}\] (Option D)

Note: First of all we have to remember the formulae \[r=\dfrac{R}{2}\] where “r” is radius and “R” is the diameter of the gas cylinder. Sometimes students forget to calculate the radius and solve the problem with diameter. So we have to find the radius to make this problem solved. Lastly we have to calculate total surface area by adding curved surface area and base surface area. Sometimes students forget to calculate total surface area and evaluate the problem with curved surface area. Students can also eliminate options B and C since their units do not match with that of area.