Question

A gardener has a cultivated plot that measures 4 feet by 6 feet. Next year, she wants to double the area of her plot by increasing the length and width by x feet. Calculate the value of x.
A. 2
B. 1
C. 3
D. 4

Answer 1

Hint: We will use formula \[area\text{ }of\text{ }rectangle\text{ }=\text{ }length\text{ }\times \text{ }breadth\] to form the new equation as $\left( x+4 \right)\left( x+6 \right)$ and then we will equate it to $2\times \left( 4\times 6 \right)=48$, that is, $\left( x+4 \right)\left( x+6 \right)=48$. We will then find ‘x’ by solving this quadratic equation.

Complete step-by-step answer:
It is given in the question that the dimensions of the garden in first year are 4 feet by 6 feet. We are assuming that length is 4 feet and breadth is 6 feet.
Now, the gardener wants to double the area of her plot by increasing the length and width by ‘x’ feet then we have to calculate the value of x.
We know that area of rectangular plot can be found using formula \[area\text{ }of\text{ }rectangle\text{ }=\text{ }length\text{ }\times \text{ }breadth\].

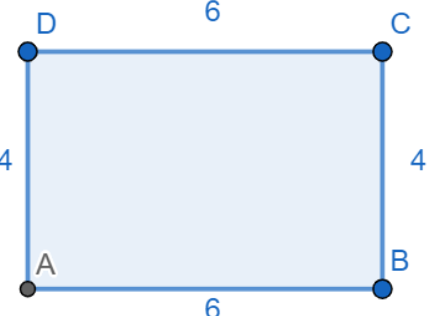
So, the area of the rectangular plot in first year will be $6feet\times 4feet=24feet\text{ }square$.
We know that the gardener wants to double the area of the rectangular plot next year. So, the area of the plot next year will be $24\times 2=48feet\text{ }square$. Also, she wants to increase the length and width by x feet to get the area as 48 square feet,

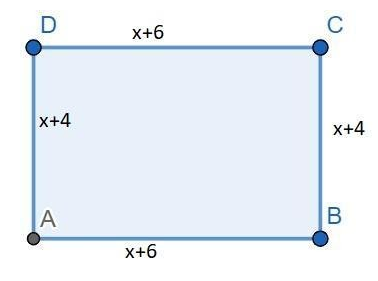
that is, $\left( x+4 \right)\left( x+6 \right)=48$
Solving further by opening brackets, we get
${{x}^{2}}+6x+4x+24=48$
Solving further, we get
${{x}^{2}}+10x-24=0$
Splitting the middle term further, we get,
${{x}^{2}}+12x-2x-24=0$
Taking $\left( x+12 \right)$ as a common factor, we get,
$x\left( x+12 \right)-2\left( x+12 \right)=0$
Solving further, we get
$\left( x-2 \right)\left( x+12 \right)=0$
Therefore, we get the values of x as $x=2,x=-12$.
Now, we know that length and width cannot be negative, thus -12 can be neglected and thus the length and width of plot is increased by 2 feet.
Thus, option a) is the correct answer.

Note: Students may directly double the length and width to get the double area of first year, but this is not correct, if we double the length and width, then area will increase by 4 times, which is not desired in the question. So this type of mistake should not be committed in the exams.