Question

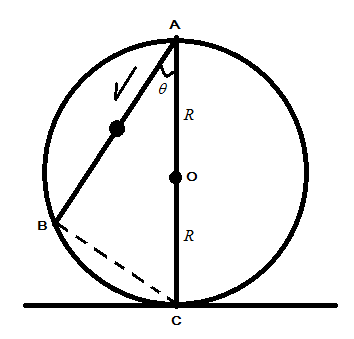
A frictionless wire AB is fixed on a sphere with radius $ R $ . A very small spherical ball slips on this wire. The time taken by this ball to slip from A to B is:

Answer 1

Hint :Here, in the given diagram AB is the frictionless wire and it is fixed, we have to apply geometric and trigonometric terms to reach the answer. Acceleration due to gravity will act along the downward direction of the small spherical ball.

Complete Step By Step Answer:
 Let us first consider the given diagram in the question i.e. AB is the wire which is fixed and friction less so we do not have to consider any friction acting while sliding the spherical ball on the wire. $ R $ is the radius of the bigger sphere with center O. Let $ g $ be the acceleration due to gravity acting along AC. But the requirement is that the component of acceleration due to gravity be $ g\cos \theta $ along AB.
So, the distance travelled by the small spherical ball in time $ t $ is
 $ AB = \dfrac{1}{2}g\cos \theta {t^2} $ ……..(using kinematic equation $ s = ut + \dfrac{1}{2}a{t^2} $
  $ u = 0 $ , $ a = g\cos \theta $ and $ s = AB $ )
Now, from $ \Delta ABC $ , $ \angle ABC = {90^0} $
 $ \therefore AB = 2R\cos \theta $ …….(by using trigonometric ratios)
Thus,
 $ 2R\cos \theta = \dfrac{1}{2}g\cos \theta {t^2} $
 $ \Rightarrow {t^2} = \dfrac{{4R}}{g} $
 $ \Rightarrow t = 2\sqrt {\dfrac{R}{g}} $
Hence, the spherical ball will take $ 2\sqrt {\dfrac{R}{g}} $ seconds to travel through AB wire under the influence of acceleration due to gravity.

Note :
We know that, if the wire is frictionless there is no need of using the frictional force components but that does not mean the gravity does not act, the gravity will still act on the spherical ball in downward direction only. We must clearly have an idea what ratio of trigonometry should be used here and always resolve the components if needed for any force acting or the acceleration as well.