Question

A force of 10 N is resolved into the perpendicular components. If the first component makes \[30{}^\circ \] with the force the magnitudes of the components are:
\[A.\,5N,\,5N\]
\[B.\,5\sqrt{2}N,\,5N\]
\[C.\,5\sqrt{3}N,\,5N\]
\[D.\,10N,\,1\sqrt{3}N\]

Answer 1

Hint: We will make use of the formulae for calculating the rectangular components of the force to solve this problem. We will substitute the given values, that is, the magnitude of the force and the angle made by the component of the force concerning the axis.
Formula used:
\[\begin{align}
  & {{F}_{H}}=F\cos \theta \\
 & {{F}_{V}}=F\sin \theta \\
\end{align}\]

Complete step-by-step solution
The formulae for computing the horizontal and the vertical components of the force are given as follows.
\[\begin{align}
  & {{F}_{H}}=F\cos \theta \\
 & {{F}_{V}}=F\sin \theta \\
\end{align}\]
Where F represents the magnitude of the force and \[\theta \] represents the angle between the components of the force and the resultant force.
From the given, we have the data as follows.
The magnitude of the force is 10 N.
The angle made by the first component of the force is, \[\theta =30{}^\circ \]
The diagram representing the horizontal and the vertical components of the force is given as follows.

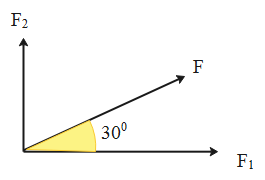
Now, we will compute the horizontal and the vertical components of the force. So, we get,
The horizontal component of the force is,
\[{{F}_{H}}=F\cos \theta \]
Substitute the given values of the magnitude of the force and angle made by the first component of the force.
\[\begin{align}
  & {{F}_{H}}=10\,\cos 30{}^\circ \\
 & {{F}_{H}}=10\times \dfrac{\sqrt{3}}{2} \\
 & {{F}_{H}}=5\sqrt{3}\,N \\
\end{align}\]
Therefore, the magnitude of the horizontal component of the force is \[5\sqrt{3}\, N\].
The vertical component of the force is,
\[{{F}_{V}}=F\sin \theta \]
Substitute the given values of the magnitude of the force and angle made by the first component of the force.
\[\begin{align}
  & {{F}_{V}}=10\,\sin 30{}^\circ \\
 & {{F}_{V}}=10\times \dfrac{1}{2} \\
 & {{F}_{V}}=5\,N \\
\end{align}\]
Therefore, the magnitude of the vertical component of the force is 5 N.
\[\therefore \] The magnitudes of the components of the force are \[5\sqrt{3}\,N\] and 5 N.
As, the values of the magnitudes of the components of the force are \[5\sqrt{3}\,N\] and 5 N, thus, option (C) is correct.

Note: The formulae for calculating the rectangular components of the force should be known to solve this type of problem. The units of the parameters should be taken care of. Using the diagram makes it easier to understand the concept.