Question

A force F is applied along the length of a rod of transverse sectional area A. The normal stress to a section PQ inclined $\theta$ to transverse section is:

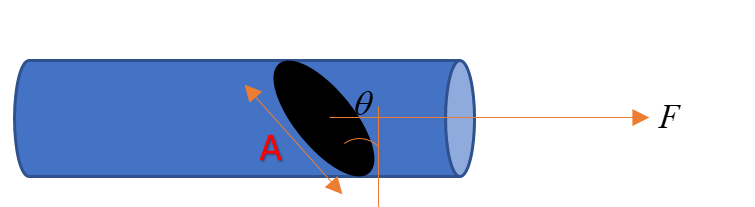
$\text{A.}\quad \dfrac{Fsin\theta}{A}$
$\text{B.}\quad \dfrac{Fcos\theta}{A}$
$\text{C.}\quad \dfrac{Fsin2\theta}{2A}$
$\text{D.}\quad \dfrac{Fcos^2\theta}{A}$

Answer 1

Hint: Stress is defined as the force per unit area produced in a body when subjected to an external force. Stress is a scalar quantity which is defined as the ratio of force acting perpendicular to the area (Normal force) of which force is applied.
Formula used:
$Stress = \dfrac{F_N}{A}$

Complete answer:
In the question, it is given that force ‘F’ is acting on the rod along the length. That means the force is not acting in direction perpendicular to the force of surface area. Hence we have to take the component of force in the direction perpendicular direction of the area under consideration, as shown by $F_N$ in the figure:

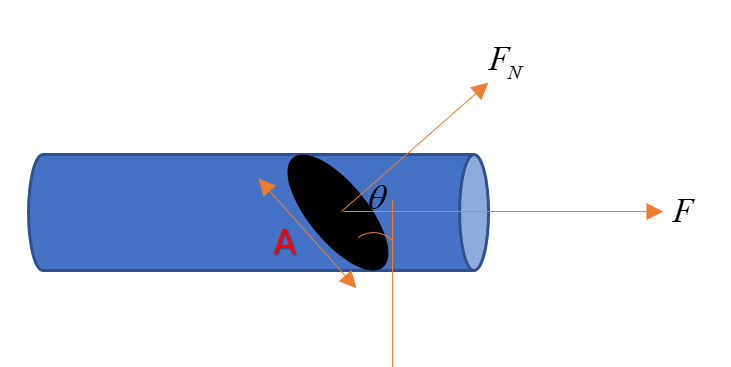
From the figure, we can write:
$F_N = F cos\theta$
Also it is given that the area ‘A’ is a transversal area. Thus the stress produced is given by:
$stress = \dfrac{Fcos\theta}{A}$

So, the correct answer is “Option B”.

Additional Information:
 Note, it is given in the question that the area ‘A’ is a transitional area and not the cross sectional area. Also the area is a vector quantity. Hence we could take the component of the area along any direction. If we’re given the area of cross section as ‘$A_1$’, than the transitional area will be ‘$A/cos\theta$’ and in that case, $stress = \dfrac{F}{A} cos^2 \theta$.

Note:
We should note that it is not the external force actually which causes the stress in the bar. It’s only in case of the bar when it is at rest. Suppose it is moving, we can’t take the force as external force. The actual cause of stress is the internal force that the molecules of the bar apply to each other.