Question

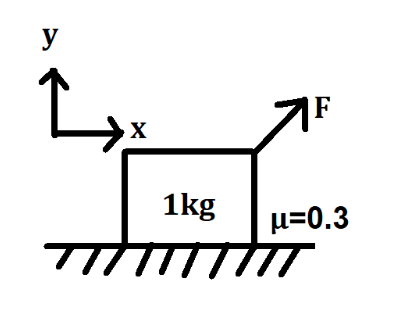
A force $ {\text{F}} = {\text{i}} + 4{\text{j}} $ acts on the block shown. The force of friction acting on the block is:
(A) $ - i $
(B) $ - 18i $
(C) $ - 2.4i $
(D) $ - 3i $

Answer 1

Hint: A vector of force is a representation of a force which has both magnitude and direction. This is opposed to simply giving the force magnitude, which is referred to as a scalar quantity. A vector is typically represented in the direction of the force by an arrow and with a length proportional to the magnitude of the force.

Formula used:
We will use the following formula to solve this question:
 $ {f_s} = \mu N $
Where
 $ {f_s} $ is the maximum frictional force that can happen of a force $ F $ is applied
 $ \mu $ is the coefficient of friction
 $ N $ is the normal force

Complete step by step answer:

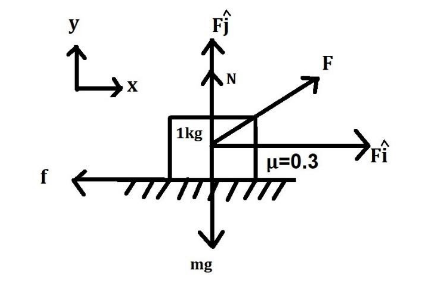
According to the question, the mass of the body is $ 1kg $
Let us suppose $ g = 10m/{s^2} $
Then the weight of the system will be $ mg = 1 \times 10 = 10N $
We can breakdown all the forces acting on the body as per the figure above
Force in the X-axis is $ F\hat i = 1N\hat i $
Force in the Y-axis is $ F\hat j = 4N\hat j $
We can see that along Y-axis, the system is in equilibrium
Now we will balance all the forces action along the Y-axis
So, we get
 $ F\hat j + N = mg $
 $ \Rightarrow N = mg - F\hat j $
Now we will put the values in the equation above to get,
 $ \therefore N = 10 - 4 = 6N $
Then the maximum frictional force that can be applied if a force $ F $ is applied,
 $ {f_s} = \mu \times N $
 $ \Rightarrow {f_s} = 0.3 \times 6 $
So, we get
 $ \therefore {f_s} = 1.8N $
Also, force in X-axis is $ 1N $
And the maximum frictional force that can be applied is $ 1.8N $
Therefore, the force is not enough to overcome the frictional force
So, the frictional force will be equal but opposite to the applied force
Hence, $ {f_s} = - i $ Correct option is (A.)

Note:
A major feature of force vectors is that, according to the application of the force, they can be broken into components. Vector components are generally perpendicular to each other, although a parallelogram configuration can also be used.