Question

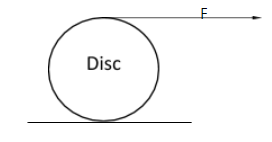
A force F acts tangentially at the highest point of a disc of mass m kept on a rough horizontal plane. If the disc rolls without slipping, the acceleration of centre of the disc is:

A. $\dfrac{{2F}}{{3m}}$
B. $\dfrac{{10F}}{{7m}}$
C. $0$
D. $\dfrac{{4F}}{{3m}}$

Answer 1

Hint: The force $F$ acting on the sphere moves it towards right. The contact point between force and sphere will slip towards the right. So the static friction on the sphere will act towards the left.

Complete step by step solution:
When a disc is rolling on a plane without slipping, the point of contact of the disc with the plane does not move.
Let the Radius of the disc = $r$
Linear acceleration = $a$
A rolling disc velocity $v$ is directly related to its angular velocity $\omega$ given as:
\[v = r\omega \], where $r$ is the radius of disc and $v$ is its linear velocity.
If we differentiate the above equation with respect to time we get linear acceleration:
$a = r\alpha $
For the case of rolling without slipping, the above equation relates the acceleration of the center of the disc to the angular acceleration $\alpha$ of the wheel.
​For linear motion apply Newton's Second Law for horizontal forces :
$F - f = ma$$F - f = ma$--- (1)
Where $f$ is the frictional force,
For rotational motion, torque about centre of disc
\[\tau = I\;\alpha \], where $I$ is the moment of inertia of the disc.
Here moment of inertia of the disc,
\[I = \dfrac{1}{2}m{r^{^2}}\]
So torque about centre of the disc,
\[\tau = \left( {\dfrac{1}{2}m{r^{^2}}} \right)\left( {\dfrac{a}{r}} \right)\]
Now apply Newton's Second for torques :
$F + f = \dfrac{1}{2}ma$_ _ _ _ (2)
From equations (1) and (2) adding, we get
$\Rightarrow 2F = \dfrac{3}{2}ma$
After solving, we get
$a = \dfrac{{4F}}{{3m}}$

$\therefore$The acceleration of centre of the disc is $a = \dfrac{{4F}}{{3m}}$

Note:
The frictional force to be pointing forward since the tensional force would produce a torque that rotates the cylinder clockwise, which produces a tendency for the bottom of the cylinder to move backward relative to the ground. Hence, the net force would be the sum of the frictional force and the tensional force (bigger than the tensional force along). Notice that the friction is static friction since there’s no slip, which would mean that the bottom of the wheel is momentarily at rest relative to ground.