Question

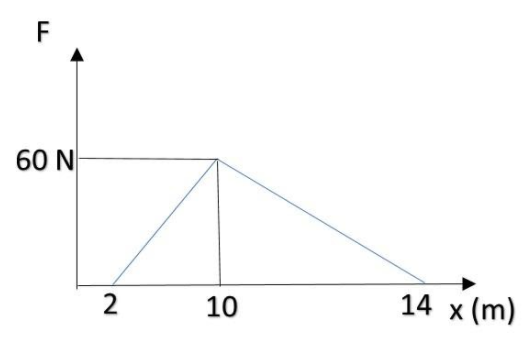
A force acts on a body and displaces it in its direction. The graph shows the relation between the force and displacement, the work done by the force between x = 10 m and x = 14 m is:

A. 420 J
B. 360 J
C. 840 J
D. 120 J

Answer 1

Hint: When a force is acted upon a body, it tends to change its state of motion or rest. If the body on which the force is acting is at rest, then the force will change its various parameters like acceleration, position, and velocity. And if it is so, then we can say that force has done some sort of work on the body which displaced the body.

Formula used: $\int F . ds = W$

Complete step-by-step solution:
Here, we must note that work is defined as the dot product of force and displacement. It means that the work done on a body is also dependent upon the angle between force and displacement. Mathematically, $W = F.s = Fs cos\theta$
Hence we can see, if the angle between force and displacement is $90^\circ$ then no work is done on the body.
Now, the term $\int F . ds$ represents the area under the F-s curve, taken between the given values of coordinates of position.
Now, if we want to find the work done by the force to cause some displacement in the body, we just have to find the area between curves.
Hence, we’re supposed to find the area between $x= 10m$ to $x= 14m$.
Hence area of F-s curve under x = 10 m and x = 14 m is:
Area of triangle = $\dfrac 12 bh$
Where base (b) = $14 – 10 = 4 m$
And height (h) = $60 \text{N}$
Area = $\dfrac 12 60\times 4 = 120 J$
Hence the work done on the body is 120J, option D. is correct.

Note: We can also proceed by calculating the writing the equation of line made by force and displacement and then write F in terms of displacement and then apply $\int F . ds = W$to integrate between the limits $x = 10 m$ to $x = 14 m$.