Question

A force \[2\hat i + \hat j - \hat k\] newton acts on a body which is initially at rest. If the velocity of the body at the end of 20 seconds is \[4\hat i + 2\hat j + 2\hat k\]m/s, the mass of the body
A) 20 kg
B) 15 kg
C) 10 kg
D) 5 kg

Answer 1

Hint: Any physical quantity having magnitude as well as direction is known as vector quantity. For example, Force, velocity etc. It is denoted by \[\vec v\]the arrow sign on the head defines it as vector quantity.
Any physical quantity having only magnitude is known as scalar quantity. For example, mass, speed etc.
Force is defined as any push or pull experienced by a body. It is also defined as the change in momentum per unit time. Its S.I unit is Newton (N).
\[\vec F = \dfrac{{md\vec v}}{{dt}} = m\vec a\]
Where Acceleration (a) = \[ = \dfrac{{d\vec v}}{{dt}}\]
\[\hat i,\hat j\;and\;\hat k\]are the unit vectors in x, y and z coordinates respectively.
Magnitude of any vector quantity \[\vec V = a\hat i + b\hat j + c\hat k\] is given by,
\[|\vec V| = \sqrt {({a^2} + {b^2} + {c^2})} \]

Complete step by step solution:
Given, initially body is at rest that is \[{V_1} = 0m/s\] (at time \[{t_1}\]= 0 )
Aso Force applied, \[\vec F = 2\hat i + \hat j - \hat k\]
As we know that magnitude is given by the formula \[|\vec V| = \sqrt {({a^2} + {b^2} + {c^2})} \]
Thus, magnitude of the Force applied will be
\[|\vec F| = \sqrt {{2^2} + {1^2} + {{( - 1)}^2}} = \sqrt 6 \]
Now the change in velocity after 20 seconds ( \[{t_2}\]) = \[4\hat i + 2\hat j + 2\hat k\]
That is \[{\vec V_2} = 4\hat i + 2\hat j + 2\hat k\],
Thus magnitude of the velocity will be,
\[|{\vec V_2}| = \sqrt {{4^2} + {2^2} + {2^2}} = \sqrt {24} = 2\sqrt 6 \]
As we know that \[\vec F = \dfrac{{md\vec v}}{{dt}}\]
\[ \Rightarrow \vec Fdt = md\vec v\]

Integrating both sides we get,
\[\begin{gathered}
\int\limits_{{t_1}}^{{t_2}} {\vec Fdt = \int\limits_{{V_1}}^{{V_2}} {md\vec v} } \\
 \Rightarrow \vec F[t]_{{t_1}}^{{t_2}} = m[\vec V]_{{V_1}}^{{V_2}} \\
 \Rightarrow \vec F({t_2} - {t_1}) = m({{\vec V}_2} - {{\vec V}_1}) \\
\end{gathered} \]

Putting all the values and taking mod in both sides we get,
\[\begin{gathered}
  |\vec F|(20 - 0) = m|({{\vec V}_2} - 0)| \\
  i.e.\sqrt 6 \times 20 = m \times 2\sqrt 6 \\
\end{gathered} \]
Hence, \[m = 10kg\]

Clearly option ( C ) is the correct answer i.e mass of the body is10 kg .

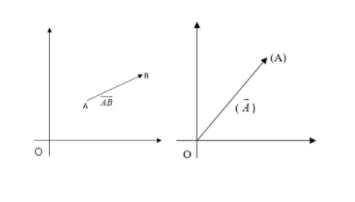
Note: If any vector is denoted by \[\overrightarrow {AB} \] then its direction is from point A to point B.
And if it is denoted by \[\overrightarrow A \]then it is pointed to point A from the origin O when represented in the Cartesian coordinate system.