Question

A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9cm, 28cm and 35cm (see figure). Find the cost of polishing the tiles at the rate of 50 p per $c{m^2}.$

Answer 1

Hint- In this question, we will approach the problem in such a way that we will find the semi perimeter of the tile and then find the area of the tile using the Heron’s formula and then multiply that with 16 because there are 16 triangular tiles in total and on the basis of the total area we can calculate the cost of polishing all the tiles.

Complete step-by-step solution -

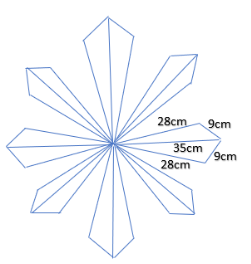
Here, let us suppose sides of the triangular portion be a, b and c respectively.
Now, a = 35cm, b = 28cm, c = 9cm
We know that semi-perimeter of tile $ = \dfrac{{a + b + c}}{2}$
On substituting the values of a, b and c we get,
Semi-perimeter of tile $ = \dfrac{{35cm + 28cm + 9cm}}{2} = \dfrac{{72cm}}{2} = 36cm$
Now using Heron's formula,
Area of the triangular tile $ = \sqrt {s(s - a)(s - b)(s - c)} $
$ = \sqrt {36cm(36cm - 35cm)(36cm - 28cm)(36cm - 9cm)} = \sqrt {36cm \times 1cm \times 8cm \times 27cm} $
$ = \sqrt {36cm \times 1cm \times 8cm \times 27cm} = \sqrt {7776c{m^4}} = 88.18c{m^2}$
So, the area of 1 tile is equal to $88.18c{m^2}$
Now, there are 16 tiles in total so the area of 16 tiles is equal to area of 1 tile multiplied by 16
$ = 88.18c{m^2} \times 16 = 1410.88c{m^2}$
Also, we have been given that the cost of polishing the tiles per $c{m^2}$ area is 50p or Rs. 0.5
Cost of polishing $1410.88c{m^2}$ area $ = Rs.0.5 \times 1410.88 = Rs.705.44$
Hence, the cost of polishing the tiles at the rate of 50 p per $c{m^2}$ is Rs. 705.44

Note – For such types of questions, just keep in mind that if all the sides of a triangle are given we can calculate the area of the triangle by using the hero’s formula which simply states that first we have to calculate the semi-perimeter of the triangle by using $s = \dfrac{{a + b + c}}{2}$ and then use that semi perimeter of the triangle to calculate the area of the triangle as area $ = \sqrt {s(s - a)(s - b)(s - c)} $. Students are mostly using the formula $\dfrac{1}{2} \times \text{Base}\times \text{Height} $ which makes the solution complicated, so this thing should be avoided in case when the side lengths are given.