Question

A flooring tile has the shape of the parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area $1080{{m}^{2}}$.

Answer 1

Hint: First, we should change the units of the area of the parallelogram from metre to centimetre square to get both the units in one dimension by using the formula $1{{m}^{2}}=10000c{{m}^{2}}$. Then, we will find the area of the parallelogram by using height and base given as $A=b\times h$. Then, to get the number of tiles required to cover the entire floor, we need to divide the total area of the floor with the area of the single tile.

Complete step-by-step answer:
In this question, we are given the fact that flooring tile has the shape of the parallelogram with base as 24 cm and its corresponding height as 10 cm.
So, the figure to visualise the above statement is:

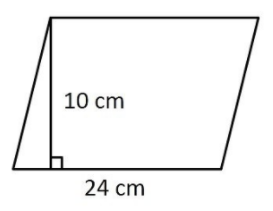
Now, the most important thing is that the area of parallelogram is given in metres square and both the sides are given in centimetre which is different.
So, we need to change the any one of them by using the relation as:
1 meter= 100 centimetre
$\begin{align}
  & 1{{m}^{2}}=100\times 100c{{m}^{2}} \\
 & \Rightarrow 1{{m}^{2}}=10000c{{m}^{2}} \\
\end{align}$
So, by using the above relation we can get the area of the parallelogram in $c{{m}^{2}}$.
Now, to get the area of parallelogram in $c{{m}^{2}}$, multiply the given area with the above relation as:
$\begin{align}
  & 1080{{m}^{2}}=1080\times 10000c{{m}^{2}} \\
 & \Rightarrow 1080{{m}^{2}}=10800000c{{m}^{2}} \\
\end{align}$
Now, we will find the area(A) of the parallelogram by using the formula where b is base and h is height as:
$A=b\times h$
Now, by substituting the value of the base as 24 cm and height as 10 cm to get the area of the parallelogram which is a tile as:
$\begin{align}
  & A=24cm\times 10cm \\
 & \Rightarrow A=240c{{m}^{2}} \\
\end{align}$
Now, to get the number of tiles required to cover the entire floor, we need to divide the total area of the floor with the area of the single tile calculated above.
So, to divide the area of the floor with the area of the one tile as:
$\dfrac{10800000}{240}=45000$
Hence, 45000 tiles are required to cover the entire floor area.

Note: The major mistake we will make while solving these kinds of questions is that we don’t give attention to the units of the area and sides of the parallelogram which need to be the same. As if in this question if we proceed with the given dimensions and calculate the number of tiles by dividing the total area of the floor with the area of the single tile as:
$\dfrac{1080}{240}=4.5$
The above calculation is totally wrong as 1080 has the unit as ${{m}^{2}}$ and 240 has units as $c{{m}^{2}}$.