Question

A flag-staff of height h stand on the top of a school building. If the angles of elevation of the top and bottom of the flag-staff have measure $\alpha $ and \[\beta \] are respectively from a point on the ground, prove that the height of the building is $\dfrac{htan\beta }{tan\alpha -tan\beta }$

Answer 1

Hint: Here we use the concept of Heights and Distances combined with Trigonometry.
Required Formula:
$\tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side}$
Given: Height of flag-staff on the top of a school building is \[h\] .
Angles of elevation of the top and bottom of the flag-staff are $\alpha $ and \[\beta \] are respectively.

Complete step-by-step answer:
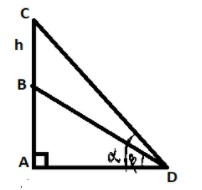
Let AB be the height of a school building.
 (A, B) are the top and bottom points of school building
Height of the flag staff is \[h\] which is CB.
Let D be the observation point from the ground to the flag staff , such that angle of elevation of top and bottom are $\alpha $ and \[\beta \] are respectively
From ΔABD,
\[tan\beta =\dfrac{BA}{AD}\]
​\[\Rightarrow AB=ADtan\beta \]
From ΔCAD,
\[\begin{align}
  & tan\alpha ~=\dfrac{CA}{AD} \\
 & AC=ADtan\alpha \\
\end{align}\] ​
\[\begin{align}
  & h+AB=ADtan\alpha \\
 & h+AD\tan \beta =ADtan\alpha \\
 & h=ADtan\alpha -AD\tan \beta \\
 & h=AD(tan\alpha -\tan \beta ) \\
 & AD=\dfrac{h}{tan\alpha -\tan \beta } \\
\end{align}\]
Since ,
$\begin{align}
  & AB=AD\tan \beta \\
 & AB=\dfrac{h}{tan\alpha -\tan \beta }\left( \tan \beta \right) \\
\end{align}$
Therefore height of the school building is $\dfrac{htan\beta }{tan\alpha -tan\beta }$
Hence proved.

 Note: In such type of questions which involves concept of Heights and Distances combined with Trigonometry drawing a figure according to the question is needed. Frame the equations accordingly to get the required value.