Question

A fixed point at a perpendicular distance ‘a’ from a fixed straight line and a point moves so that its distance from the fixed point is always equal to its distance from the fixed line. Find the equation to its locus, the axes of coordinates being drawn through the fixed point and being parallel and perpendicular to the given line.

Answer 1

Hint: Take the fixed point O as origin with coordinate (0, 0). Assume the moving or variable as point P with coordinates (h, k). Find distance of P from O, PO. Then, find the distance of variable point P (h, k) from the line. Equate both of these distances found.

Complete step-by-step answer:
A fixed point is at a perpendicular distance 'a' from a fixed straight line.

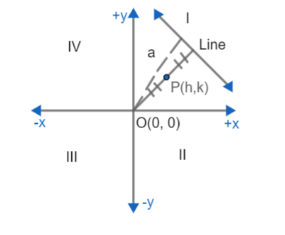
Point P(h, k) can be at any coordinate plane with coordinates (h, k) in I quadrant, (h, -k) in II, (-h, -k) in III and (-h, k) in IV quadrant.
There is one variable point which keeps moving such that, it is equidistant from both fixed line and fixed point.
Suppose, the fixed point is origin (0, 0) = O (0, 0) the variable point is P with coordinate (h, k) i.e. P (h, k) in I quadrant for less complexity.
We need to find the locus of the variable point P (h, k), locus is the equation path the point covers based on the given condition.
We have fixed point O (0, 0) and variable point P (h, k) finding out the distance between these two points:
Distance between two points is calculated as,

\[AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Here, we have
\[\text{PO=}\sqrt{{{\left( h-0 \right)}^{2}}+{{\left( k-0 \right)}^{2}}}=\sqrt{{{h}^{2}}+{{k}^{2}}}\]
The fixed line is parallel and perpendicular to the line connecting P and O, which tells us that it is parallel to x axis and perpendicular to y-axis. It is at a distance 'a' from the fixed point O.
So, we get the equation is y = a.
Now, calculating the distance of the fixed line from variable point P.
We know that the distance between a line and a point is calculated as:
Assume line = ax+by+cz = d, point = (h, k)
\[\text{Distance= }\left| \dfrac{axh+bxk+d}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|\]
So, here we have \[\text{Distance= }\left| \dfrac{0\left( h \right)+1\left( k \right)-a}{\sqrt{{{0}^{2}}+{{1}^{2}}}} \right|=\left| k-a \right|\]
It is given that, distance of variable point P (h, k) from fixed point O (0, 0) and fixed line is equal. So, we will equate them as below,
\[\begin{align}
  & \text{Distance=PO} \\
 & \Rightarrow \left| k-a \right|=\sqrt{{{h}^{2}}+{{k}^{2}}} \\
 & \Rightarrow {{h}^{2}}+{{k}^{2}}={{\left( k-a \right)}^{2}} \\
 & \Rightarrow {{h}^{2}}+{{k}^{2}}={{k}^{2}}+{{a}^{2}}-2ka \\
 & \Rightarrow {{h}^{2}}-{{a}^{2}}+2ak=0 \\
 & \Rightarrow {{h}^{2}}+2ak-{{a}^{2}}=0 \\
\end{align}\]
Replacing h by x and k by y to generalize the locus, we get
\[\Rightarrow {{x}^{2}}+2ay-{{a}^{2}}=0\]
This is the required locus of variable point P (h, k).

Note: Fixed point need not to be origin, it can be any point, just for the sake of less complexity it is taken as origin (0, 0). While applying the formulas, we must be careful not to make any silly mistakes. The main point is to equate the distances and get the locus.