Question

(a). Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be $\dfrac25MR^2$, where M is the mass of sphere and R is the radius of the sphere.

Answer 1

Hint: To find the moment of inertia of any shape about an unknown axis, first we need to know the moment of inertia of the shape about an axis either perpendicular to it or parallel to it. If we know the moment of inertia of a shape about an axis passing through the centre of mass of the body, then we can find the moment of inertia about any axis parallel to it by the use of parallel axis theorem.

Formula used:
${ I }_{ axis }={ I }_{ com }\ +\ Md^{ 2 }$ [ Statement of parallel axis theorem ]
Where M is the mass of the body and d is the distance of the axis from the centre of mass ( COM ) of the body.

Complete step-by-step answer:
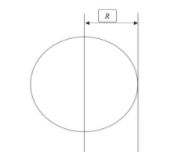
Given that moment of inertia of the sphere about its diameter is $\dfrac25MR^2$ . Since diameter always passes through the centre of mass of a sphere hence $I_{com}=\dfrac25MR^2$. As distance of diameter of sphere from its tangent (the parallel one) will always be equal to the radius R hence $d=R$.
Hence on putting the values, ${ I }_{ axis }=\dfrac{2}{5}MR^2 +\ MR^{ 2 }$= $\dfrac{7}{5}MR^2$

Note: While using the Parallel axis theorem, one axis should always be the one passing through the centre of mass. Chance of mistakes is high if one avoids this information. Students are advised to learn the moment of inertia of commonly used shapes for example: Disc, sphere, etc. $\dfrac25MR^2$is the moment of inertia of a solid sphere.