Question

(a) Find acceleration.
          (b) Find tension in the string.

Answer 1

Hint:The force acting on a body creates acceleration. Now if the body attached to the string feels force, then, there originates a tension on the string. These tension pulls the body attached to the other end of the string and thus produces an acceleration to the whole system.

Step by step answer:
Formulae Used:
If a force $F$ acts on an object of $m$ and produces acceleration $a$ then you have the expression
$F = ma$
Given:
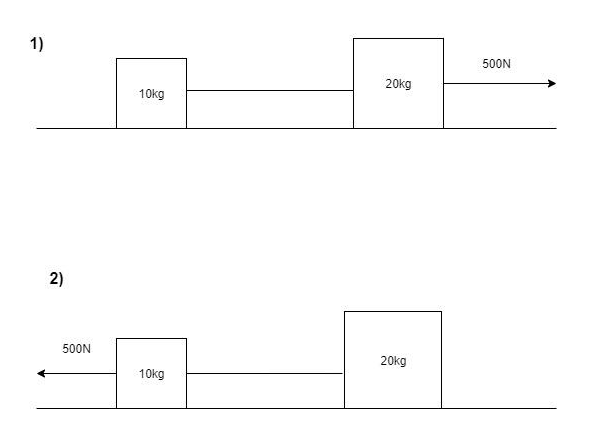
For the figure (1):
The force $F$ acted upon is $500N$.
The mass of the immediately attached body is $M = 20kg$.
The mass of the body attached to the other end is $m = 10kg$.

For the figure (2):
The force $F$ acted upon is $500N$.
The mass of the immediately attached body is $m = 10kg$.
The mass of the body attached to the other end is $M = 20kg$.
To get: (a) The acceleration.
     (b) The tension in the string.
Step 1:
Let the tension on the string be $T$. Let the acceleration on the system is $a$.
For the figure (1) you can equate the forces acting on the system.
$500 - T = 20a$
$T = 10a$
Putting eq (3) in eq (2) you have
$
  500 - 10a = 20a \\
   \Rightarrow 30a = 500 \\
   \Rightarrow a = \dfrac{{500}}{{30}} = 16.67 \\
 $
$\therefore a = 16.67m/{s^2}$
So, calculate the value of $T$
$T = 16.67 \times 10 = 166.7$
$\therefore T = 166.7N$
Step 2:
Let the tension on the string be $T$. Let the acceleration on the system is $a$.
For the figure (2) you can equate the forces acting on the system.
$500 - T = 10a$
$T = 20a$
Putting eq (3) in eq (2) you have
$
  500 - 20a = 10a \\
   \Rightarrow 30a = 500 \\
   \Rightarrow a = \dfrac{{500}}{{30}} = 16.67 \\
 $
$\therefore a = 16.67m/{s^2}$
So, calculate the value of $T$
$T = 16.67 \times 20 = 333.4$
$\therefore T = 333.4N$

Final Answer:
From figure (1),
a) The acceleration of the system is $16.67m{s^{ - 2}}$.
b) The tension on the string is $166.7N$.
From figure (2),
a) The acceleration of the system is $16.67m{s^{ - 2}}$.
b) The tension on the string is $333.4N$.

Note: The tension on the string plays a crucial role in the system. The end where the force is applied the tension on the string is generated. Similarly due to this tension a reaction is generated from the other end of the string. Here no friction is considered. So, you should take the acceleration of the whole system the same.