Question

A farmer is having a field in the form of a parallelogram PQRS. He took any point A on RS and joined it to point P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should he do it?

Answer 1

Hint: First, need to construct the figure as the parallelogram PQRS having a point A on the side RS and it is joined with P and Q. Then, triangle APQ and parallelogram PQRS are on the same base which is PQ and between the same parallels PQ and RS gives the property $ ar\left( APQ \right)=\dfrac{1}{2}ar\left( PQRS \right) $ . Then, we get the area of the remaining two triangles that are triangle PSA and triangle ARQ is combined equivalent to area of the triangle APQ.

Complete step-by-step answer:
In this question, we are supposed to find a lot of things but before we need to construct the figure as per instructions.
So, the parallelogram PQRS having a point A on the side RS and it is joined with P and Q as:

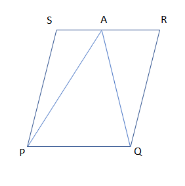
Now, from the figure it is clearly visible that the figure is divided into three triangles.
Since, triangle APQ and parallelogram PQRS are on the same base which is PQ and between the same parallels PQ and RS.
So, it gives the property that:
 $ ar\left( APQ \right)=\dfrac{1}{2}ar\left( PQRS \right) $
Now, rearranging the above expression, we get:
 $ 2ar\left( APQ \right)=ar\left( PQRS \right) $
But from the figure it is clear that:
 $ ar\left( PQRS \right)=ar\left( PSA \right)+ar\left( APQ \right)+ar\left( ARQ \right) $
Now, by substituting the value of the area of parallelogram PQRS as:
 $ \begin{align}
  & 2ar\left( APQ \right)=ar\left( PSA \right)+ar\left( APQ \right)+ar\left( ARQ \right) \\
 & \Rightarrow ar\left( APQ \right)=ar\left( PSA \right)+ar\left( ARQ \right) \\
\end{align} $
So, from the above expression we get the area of the remaining two triangles that are triangle PSA and triangle ARQ is combined equivalent to area of the triangle APQ.
Now, to sow wheat and pulses in equal portions of the field separately, farmer should sow wheat in $ \Delta APQ $ and pulses in other two triangles which are triangle PSA and triangle ARQ or vice-versa.

Note: Now, to solve these types of questions we need to know some of the basic properties of the triangles and parallelograms to get the desired result. So, the property used here is when the triangle and a parallelogram are on the same base and between the same parallels then the area of the triangle is half the area of that parallelogram.