Question

A farmer connected a pipe of internal diameter 20 cm from the canal into a cylindrical tank in his field which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h in how much time will the tank be filled?

Answer 1

Hint: Let us assume that in “t” hours the tank be filled by the cylindrical pipe then the volume of the water coming from the cylindrical pipe is equal to area of cross section of the pipe multiply by the rate of flow and the multiplication of this result by time “t” then equate this volume with the volume of the cylindrical tank which is calculated by using the formula for the volume of cylinder which is equal to $ \pi {{r}^{2}}h $ where “r” is the radius of the cylinder and “h” is the height of the cylinder.

Complete step-by-step answer:
Let us assume that the pipe is taking “t” hours to fill the cylindrical tank. Then the volume of the water flown from the canal to the cylindrical tank is equal to the multiplication of area of the cross section of the pipe with the rate at which water is flowing through the pipe and with the time “t”.
Area of cross section of the cylindrical pipe with diameter 20 cm is equal to:
 $ \pi {{r}^{2}} $
In the above expression, “r” is the radius of the pipe which we can calculate by dividing the diameter by 2 so dividing the diameter of 20 cm by 2 we get the radius as 10 cm. Now, substituting this value of radius in the above expression we get,
 $ \pi {{\left( 10 \right)}^{2}}c{{m}^{2}} $
We are converting the above area in $ c{{m}^{2}} $ to the $ {{m}^{2}} $ by multiplying the above result by .0001.
 $ \begin{align}
  & 100\pi \left( 0.0001 \right){{m}^{2}} \\
 & =0.01\pi {{m}^{2}} \\
\end{align} $
We have given the rate in km/h so we will convert this rate into m/h by multiplying the rate by 1000 so the rate of flow of water through the pipe is equal to:
 $ \begin{align}
  & 3\times 1000\text{ m/h} \\
 & =3000\text{ m/h} \\
\end{align} $
Now, we are going to find the volume of flow of water from the pipe.
 $ \begin{align}
  & 0.01\pi \left( 3000 \right)t\text{ }{{\text{m}}^{3}} \\
 & =30\pi t\text{ }{{\text{m}}^{3}} \\
\end{align} $ …………. Eq. (1)
In the below figure, we have shown a cylinder of radius “r” and height “h”.

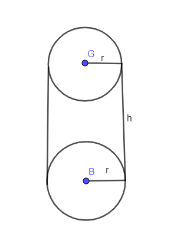
The volume of the cylindrical tank is calculated by using the formula for volume of the cylinder which is given as:
 $ \pi {{r}^{2}}h $
In the above expression, “r” is the radius and “h” is the height of the cylinder.
We have given that the diameter of the cylindrical tank is equal to 10 m so the radius of the cylinder will be half of the diameter i.e. 5 m and the height of the cylinder is given as 2 m.
Substituting the values of r and h that we have calculated above in the volume of the cylinder we get,
 $ \begin{align}
  & \pi {{\left( 5 \right)}^{2}}\left( 2 \right) \\
 & =\pi 50\text{ }{{\text{m}}^{3}}......Eq.(2) \\
\end{align} $
Now, equating the volume of the water flown through the pipe and the volume of cylindrical tank we get the value of “t” which is shown below:
 $ 30\pi t\text{ }{{\text{m}}^{3}}=\pi 50\text{ }{{\text{m}}^{3}} $
In the above equation $ \pi \And {{m}^{3}} $ will be cancelled on both the sides of the above equation.
 $ 30t=50 $
Dividing 30 on both the sides we get,
 $ \begin{align}
  & t=\dfrac{5}{3} \\
 & \Rightarrow t=1.66\text{ hours} \\
\end{align} $
Hence, the cylindrical pipe will take $ 1.66\text{ hours} $ to fill the tank.

Note: You can also convert the time that you have got above in minutes by multiplying the time $ 1.66\text{ hours} $ to 60. So, on multiplication we get the time as:
 $ \dfrac{5}{3}\times 60=100\text{ minutes} $
One more thing to be taken into account is that usually in the hastiness of solving the question, students tend to forget to convert the diameter into radius. Be careful by writing the radius in area and volume not the diameter into them.