Question

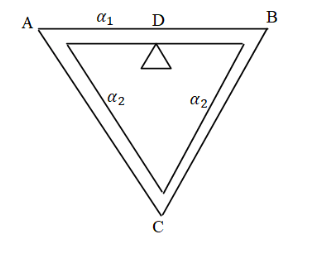
A equilateral triangle ABC is formed by joining three rods of equal lengths and D is the midpoint of AB. The coefficient of linear expansion for AB is ${\alpha _1}$and${\alpha _2}$, if distance DC remains constant for small changes in temperature is
A) ${\alpha _1} = {\alpha _2}$.
B) ${\alpha _1} = 4{\alpha _2}$.
C) ${\alpha _2} = 4{\alpha _1}$.
D) ${\alpha _1} = \dfrac{1}{2} \cdot {\alpha _2}$.

Answer 1

Hint: When a metal is heated then the molecules in the rod get excited and also there is expansion that takes place. When a rod is heated then there is expansion of the rod depending on the thermal coefficient and change of temperature. The formula of the thermal expansion can be used to calculate the relationship between the different rods that has been asked in the problem.

Formula used: The formula for the expansion of the rod is given by, ${L_1} = L\left( {1 + \alpha \Delta T} \right)$ where the change in the length is$\Delta L$,$\alpha $ is the coefficient of thermal expansion, $\Delta T$ is the change in temperature and ${L_1}$ is the new length of the rod.

Complete step by step answer:
The length DC does not change for small changes in temperature. This is given in the problem, also it is given that the length of the three rods is equal.
Let us calculate the value of DC,
As in the triangle ADC, DC is the perpendicular, AC is hypotenuse and AD is the base.
Applying the Pythagoras theorem.
$
  A{C^2} = A{D^2} + D{C^2} \\
  \Rightarrow {L^2} = {\left( {\dfrac{L}{2}} \right)^2} + D{C^2} \\
  \Rightarrow D{C^2} = {L^2} - {\left( {\dfrac{L}{2}} \right)^2} \\
  \Rightarrow D{C^2} = {L^2} - \dfrac{{{L^2}}}{4} \\
  \Rightarrow DC = \sqrt {{L^2} - \dfrac{{{L^2}}}{4}} \\
  \Rightarrow DC = \sqrt 3 \cdot \dfrac{L}{2} ………eq. (1)\\
 $
As after change in the temperature the length DC is constant and DC depends upon the lengths of AD and AC. Let us replace the value for change in temperature.
Length for DC is unchanged for change in temperature but for the change in length with change in temperature for rods AB, AC and BC.
The length of DC after change in temperature.
Since,
$
  A{C^2} = A{D^2} + D{C^2} \\
  D{C^2} = A{C^2} - A{D^2} \\
 $
Put the value of DC from the equation (1). Also the change in length of the two rods is given by AC’ and AD’.
\[
  D{C^2} = {\left( {AC'} \right)^2} - {\left( {AD'} \right)^2} \\
  {\left( {\sqrt 3 \cdot \dfrac{L}{2}} \right)^2} = {\left( {AC'} \right)^2} - {\left( {AD'} \right)^2} \\
  \dfrac{3}{4}{L^2} = {\left( {AC'} \right)^2} - {\left( {AD'} \right)^2} \\
 \]………eq. (2)
Let us calculate the new length after change in temperature,
For rod AC,
\[
  {L_1} = L\left( {1 + {\alpha _2}\Delta T} \right) \\
  AC' = L\left( {1 + {\alpha _2}\Delta T} \right) \\
 \].........eq. (3)
For rod AB,
\[
  {L_2} = L\left( {1 + {\alpha _1}\Delta T} \right) \\
  AD' = L\left( {1 + {\alpha _1}\Delta T} \right) \\
 \]………eq. (4)
Replace the value of equation (3) and (4) in equation (2).
\[
  \Rightarrow \dfrac{3}{4}{L^2} = {\left( {AC'} \right)^2} - {\left( {AD'} \right)^2} \\
  \Rightarrow \dfrac{3}{4}{L^2} = {\left[ {L\left( {1 + {\alpha _2}\Delta T} \right)} \right]^2} - \dfrac{1}{4}{\left[ {L\left( {1 + {\alpha _1}\Delta T} \right)} \right]^2} \\
  \Rightarrow \dfrac{3}{4}{L^2} = {L^2}\left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \dfrac{1}{4}{L^2}\left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right] \\
  \Rightarrow \dfrac{3}{4} = \left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \dfrac{1}{4}\left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right] \\
  \Rightarrow \dfrac{3}{4} = \dfrac{{4\left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right]}}{4} \\
  \Rightarrow 3 = 4\left[ {1 + {{\left( {{\alpha _2}\Delta T} \right)}^2} + 2{\alpha _2}\Delta T} \right] - \left[ {1 + {{\left( {{\alpha _1}\Delta T} \right)}^2} + 2{\alpha _1}\Delta T} \right] \\
  \Rightarrow 3 = 3 + 4{\left( {{\alpha _2}\Delta T} \right)^2} + 8{\alpha _2}\Delta T - {\left( {{\alpha _1}\Delta T} \right)^2} - 2{\alpha _1}\Delta T \\
  \Rightarrow 0 = 4{\left( {{\alpha _2}\Delta T} \right)^2} + 8{\alpha _2}\Delta T - {\left( {{\alpha _1}\Delta T} \right)^2} - 2{\alpha _1}\Delta T \\
 \]
As the change in temperature is small. Therefore ${\left( {\Delta T} \right)^2} \approx 0$.
\[
 \Rightarrow 0 = 4{\left( {{\alpha _2}\Delta T} \right)^2} + 8{\alpha _2}\Delta T - {\left( {{\alpha _1}\Delta T} \right)^2} - 2{\alpha _1}\Delta T \\
  \Rightarrow 0 = 8{\alpha _2}\Delta T - 2{\alpha _1}\Delta T \\
 \Rightarrow 8{\alpha _2}\Delta T = 2{\alpha _1}\Delta T \\
  \Rightarrow 4{\alpha _2} = {\alpha _1} \\
 \]

So the correct answer for this problem is option B.

Note: Students should remember the formula of the thermal expansion as this formula can be used for solving these types of problems. The change in temperature of the rod is small and therefore the square of the change in temperature is taken as zero while solving the problem students should not get confused in those steps.