Question

A drunkard walking along a road takes 5 steps forward and 3 steps backward, and so on. Each step is 1m long and takes 1s. There is a pit on the road 11m away from the starting point.
The drunkard fall into the pit after
(A) 29 steps
(B) 21 steps
(C) 37 steps
(D) 31 steps

Answer 1

Hint: We will calculate the above question on the number line to make it easy to understand. Distance between each point on line is 1km.
On the 11th point there is a pit.

Complete step by step solution: According to question : He walks 5 steps forward and 3 backward each step is of 1m and takes 1 sec. So, let's make a number line.
(1)
 

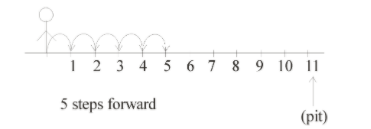
                    5 steps forward
(2)

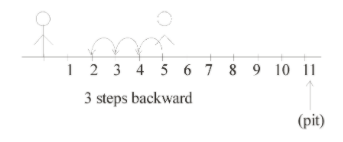
                        3 steps backwards

(3) In the above two steps he reached at point 2. But travelled $5 + 3 = 8$ steps
      So, total distance travelled by him $ = 5 - 3 = 2$
      Since 1 step takes 1 sec, therefore by taking 8 steps he took 8 sec.
      So we can say that he is moving 2 km in 8 sec.
(4) Now he will move from point 2, in the same manner. i.e., 5 forward and 3 backward.

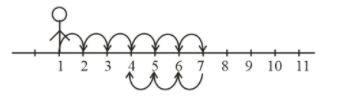
Now he is on point 4.
So, covered 4 km in total $8 + 8 = 16$ seconds.
(5) In another 8 sec he will cover another 2 km. Now he is at point 6.
i.e., he covered 6 km in total $16 + 8 = 24$ sec
(6) But from point 6 when he takes 5 steps forward he falls in a pit so can’t take backward steps.
So, in the next 5 steps he took 5 sec.
(7) Or total time taken by him is $24 + 5 = 29$ sec
Therefore, option (A) is i.e., 29 sec is the correct option

Note: We can solve the above question in this manner.
He moves 5 steps forward, 3 steps backward in 8 sec.
In this way he is 2m away from an initial position $x = 5 - 3 = 2m$ in 8 sec.
After 24 sec he will 6m away from an initial position.
He moves further 5m forward then he falls in a pit which is 11m away from the initial position.
Total time $T = 24 + 5 = 29\sec $