Question

A drop of liquid of density $\rho$ is floating half immersed in a liquid of density ‘d’. If $\sigma$ is the surface tension, then what is the diameter of the drop of the liquid?
$\text{A.} \sqrt{\dfrac{3\sigma}{g(2\rho-d)}}$
$\text{B.} \sqrt{\dfrac{6\sigma}{g(2\rho-d)}}$
$\text{C.} \sqrt{\dfrac{4\sigma}{g(2\rho-d)}}$
$\text{D.} \sqrt{\dfrac{12\sigma}{g(2\rho-d)}}$

Answer 1

Hint: Surface tension: It is the property of liquid by the virtue of which the surface of the liquid acts as a stretched membrane. In other words, the surface wants to minimize its area and hence when a body is kept on a liquid, liquid exerts a force on the touching boundary of the liquid and the body and also when a body is fully or partially immersed in a liquid, it experiences an upward force of buoyancy.

Formula used:
$F = Tl,\ F_B = dVg$

Complete step by step answer:
When we place something in a liquid, either it sinks or it floats. Every fluid exerts an upward force on objects lying inside it. This upward force is known as buoyant force or the force of buoyancy. The magnitude of this force depends only upon the density of liquid. If this force is more than the weight of the object, it will float and if the force is less than the weight of the object, it will sink. Now, as the drop is half immersed in the liquid, the force of buoyancy acting on it will be:
$F_B = gd(\dfrac12 \times \dfrac43\pi r^3) = \dfrac23 d\pi gr^3$
Now, force due to surface tension is given by:
$F = Tl = \sigma \times 2\pi r$
Since the drop is in equilibrium, the net force on the liquid is zero. Hence the weight of the drop must be balanced by the force of buoyancy and surface tension.

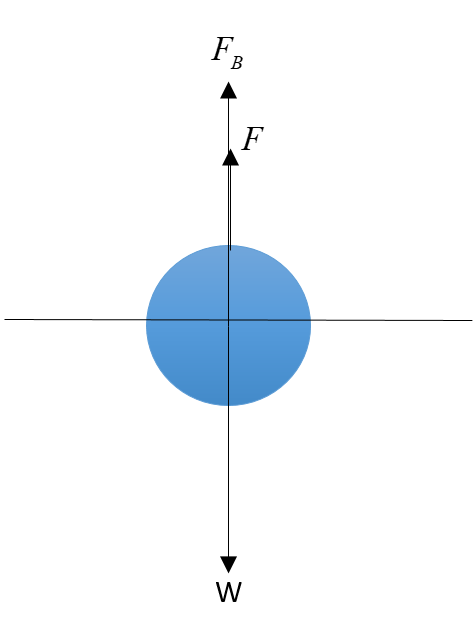
i.e. $W = F+F_B$
Now, weight W = mg = $\rho Vg$
Hence putting the values, we get;
$\rho Vg = 2\sigma \pi r + \dfrac23d\pi gr^3$
Also $V = \dfrac43\pi r^3$
$\implies \rho \dfrac43\pi r^3 g= 2\sigma \pi r + \dfrac23 d\pi gr^3$
$\implies \rho \dfrac43\pi r^3 g- \dfrac23 d\pi gr^3= 2\sigma \pi r$
$\implies 2\sigma \pi r=\dfrac23 \pi g r^3 \left( 2\rho - d\right)$
$\implies \sigma =\dfrac13 g r^2 \left( 2\rho - d\right)$
$\implies r^2 = \dfrac{3\sigma}{g(2\rho-d)}$
$\implies r = \sqrt{\dfrac{3\sigma}{g(2\rho-d)}}$

Thus, option A. is correct.

Note:
Due to the property of surface tension, the block will experience some force which is given by formula: $F = Tl$. Here, T is the surface tension and ‘l’ is the length of the object which is in contact with the fluid. Length in the sense the perimeter of the boundary which is the interface of both air and fluid.