Question

A drain cover is made from a square metal plate of side 40 cm having 441 holes of diameter 1 cm each drilled in it. Find the area of the remaining square plate.

Answer 1

Hint: We will first find the area of the square metal plate using the formula \[{{(side)}^{2}}\] and then we will find the area of one circular hole and next we will multiply it by 441 to get the total area of the holes. Finally, we will subtract both the areas to get the area of the remaining plate.

Complete step-by-step answer:
Drawing the figure from the given details in the question. In the figure we have shown only 6 holes but there are 441 similar holes.

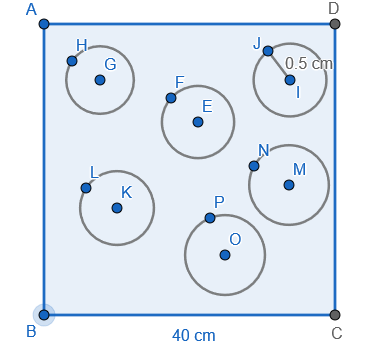
It is mentioned in the question that the drain cover is in the shape of a square with length of side as 40 cm. And we know that the area of the square is \[{{(side)}^{2}}\]. So using this information we get,
Area of the drain cover \[={{(side)}^{2}}={{(40)}^{2}}=1600\,c{{m}^{2}}........(1)\]
Now it is also mentioned in the question that the drain cover has 441 holes and holes are of 1 cm diameter which means the holes are circular in shapes. And we know that the area of the circle is \[\pi {{r}^{2}}\] and also the radius of the circle is half of the diameter and thus r is 0.5 cm. So using this information we get,
Area of each hole \[=\pi {{r}^{2}}=\dfrac{22}{7}\times {{(0.5)}^{2}}=\dfrac{11}{14}c{{m}^{2}}.........(2)\]
Now from equation (2), area of 441 holes \[=441\times \dfrac{11}{14}=346.5\,c{{m}^{2}}.......(3)\]
Hence the area of the remaining plate will be the area of the drain cover minus area of 441 holes. Doing this we get,
From equation (3) and equation (1), area of the remaining plate \[=1600-346.5=1253.5\,c{{m}^{2}}\]
Hence the area of the remaining square plate is \[1253.5\,c{{m}^{2}}\].

Note: Remembering the formula of the area of the square and the area of the circle is the key here. Also we should keep in mind that the radius is half of diameter because in a hurry we can make a mistake by substituting value of diameter in place of radius in equation (2). Writing the units is important.