Question

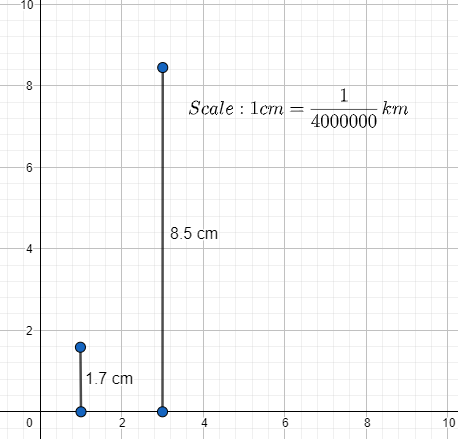
A distance of 68 km is represented on a map by 1.7 cm. What is the distance represented by 8.5 cm?

Answer 1

Hint: We should know that Scale of a map indicates the ratio of a distance on the map to the corresponding distance on the ground. In the question, it was given that a distance of 68 km is represented on a map by 1.7 cm. Now we have to scale the map. Let us assume the distance on the ground equal to x then the distance of the map is equal to 8.5 cm. In this way, we can find the value of x.

Complete step-by-step answer:
Before solving the question, we have to know that a scale is required for a map. Generally, it is not possible to represent a vast distance on a small map. So, a scale is used in a map. Scale of a map indicates the ratio of a distance on the map to the corresponding distance on the ground. By this scale, we can measure huge distances in a map.
From the question, it was given that a distance of 68 km is represented on a map by 1.7 cm. So, now we have to calculate the scale of the map. We know that the scale of a map indicates the ratio of a distance on the map to the corresponding distance on the ground.
We know that 1.7 cm is the distance on map and 68 km is the distance on the ground.
Let the scale of the map be equal to S.
So, we get
\[\Rightarrow S=\dfrac{1.7cm}{68km}\]

We know that 1 km is equal to 1000 m. We also know that 1 m = 100 cm. So, we can write
\[\begin{align}
  & \Rightarrow S=\dfrac{1.7cm}{68\times 1000\times 100cm} \\
 & \Rightarrow S=\dfrac{1.7cm}{6800000cm} \\
 & \Rightarrow S=\dfrac{17cm}{68000000cm} \\
 & \Rightarrow S=\dfrac{1}{4000000} \\
\end{align}\]
So, it is clear that the scale is equal to \[\dfrac{1}{4000000}\].
From the question, it is clear that we have to find a corresponding distance on the ground whose distance on the map is equal to 8.5 cm.
We know that the scale of a map indicates the ratio of a distance on the map to the corresponding distance on the ground.
We know that the scale of the map is equal to \[\dfrac{1}{4000000}\].
Let us assume the distance on the ground is equal to x.
\[\Rightarrow \dfrac{1}{4000000}=\dfrac{8.5cm}{xcm}\]
Now by using cross multiplication, we get
\[\begin{align}
  & \Rightarrow \dfrac{1}{4000000}=\dfrac{8.5cm}{xcm} \\
 & \Rightarrow x=(4000000)(8.5)cm \\
 & \Rightarrow x=34000000cm \\
\end{align}\]
We know that 1 km is equal to 100000 cm.
So, we get
\[x=340km\].
Hence, the distance represented by 8.5 cm is equal to 340 km.

Note: During solving the problem, students may forget to convert the kilometres to centimetres. If this is done, wrong results may occur. While solving this problem, the conversion of units is required. All the given data, must be converted into kilometres or centimetres. If this is not done the whole process may go wrong. So, students should be careful while solving this problem.