Question

A disc of mass $m$ and radius $R$ has a concentric hole of a radius $r$. Its moment of inertia about an axis through its center and perpendicular to its plane is :
A. $\dfrac{1}{2}m\left( {{R^2} + {r^2}} \right)$
B. $\dfrac{1}{2}m\left( {R - {r^2}} \right)$
C. $\dfrac{1}{2}m\left( {{R^2} - {r^2}} \right)$
D. $\dfrac{1}{2}m\left( {R + {r^2}} \right)$

Answer 1

Hint: First draw a rough diagram to solve this question. In these we have to use the moment of inertia of a disc formula. Then with the help of the formula we find the remaining moment of inertia of the disc after a small hole of radius $r$ is removed from it.

Formula used:
Moment of inertia of a disc is,
$I = \dfrac{1}{2}m{R^2}$
Where, mass of the disc is $m$ and radius of the disc is $R$.

Complete step by step answer:
As per the given problem we have a disc of mass m and radius R has a concentric hole of a radius r. We need to find the moment of inertia about an axis through its center and perpendicular to its plane. We know the moment of inertia of the disc about its axis through its center and perpendicular to its plane as,

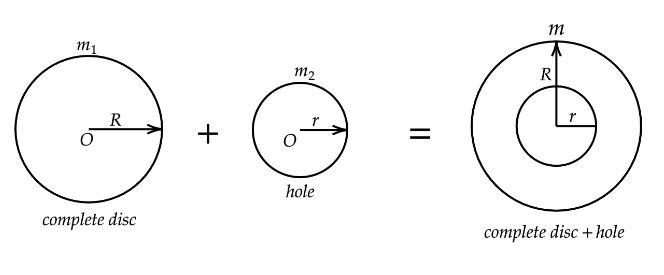
$I = \dfrac{1}{2}m{R^2}$
Now applying this formula in finding the moment of inertia of the disc with hole,
$I0 = \dfrac{1}{2}m_1{R^2} - \dfrac{1}{2}m_2{r^2}$
Where, mass of the complete disc before the concentric hole of radius r is removed is $m_1$ and radius be $R$, mass of the concentric hole is $m_2$ and radius be $r$.

We can write the mass of the remaining portion of the disc be,
$m_1 - m_2 = m \ldots \ldots \left( 1 \right)$
Also we know that mass is directly proportional to the radius of the disc.
Hence the ratio of the masses will be,
$\dfrac{{m_1}}{{m_2}} = \dfrac{{{R^2}}}{{{r^2}}}$
Rearranging the above ratio we will get,
$m_2 = \dfrac{{{r^2}}}{{{R^2}}}m_1 \ldots \ldots \left( 2 \right)$

Putting equation $\left( 2 \right)$ in equation $\left( 1 \right)$ we will get,
$m_1 - \dfrac{{{r^2}}}{{{R^2}}}m_1 = m$
$ \Rightarrow m_1\left( {1 - \dfrac{{{r^2}}}{{{R^2}}}} \right) = m$
Hence on solving further we will get,
$m_1 = \dfrac{{m{R^2}}}{{{R^2} - {r^2}}}$
Similarly,
$m_2 = \dfrac{{m{r^2}}}{{{R^2} - {r^2}}}$

Now putting $m_1$ and $m_2$ value in the above inertia $I_0$ we will get,
$I_0 = \dfrac{1}{2}\left( {\dfrac{{m{R^2}}}{{{R^2} - {r^2}}}} \right){R^2} - \dfrac{1}{2}\left( {\dfrac{{m{r^2}}}{{{R^2} - {r^2}}}} \right){r^2}$
$ \Rightarrow I_0 = \dfrac{1}{2}\left( {\dfrac{{m{R^4}}}{{{R^2} - {r^2}}}} \right) - \dfrac{1}{2}\left( {\dfrac{{m{r^4}}}{{{R^2} - {r^2}}}} \right)$
Taking out the common terms we will get,
$I_0 = \dfrac{1}{2}\left( {\dfrac{m}{{{R^2} - {r^2}}}} \right)\left( {{R^4} - {r^4}} \right) \ldots \ldots \left( 3 \right)$
Now on further solving,
$\therefore I_0 = \dfrac{m}{2}\left( {{R^2} + {r^2}} \right)$

Therefore the correct option is $\left( A \right)$.

Note: Mark that in equation $\left( 3 \right)$ we used the formula ${a^4} - {b^4} = \left( {{a^2} - {b^2}} \right)\left( {{a^2} + {b^2}} \right)$ so as to cancel the common terms present in numerator and denominator. And remember the mass of the hole can also be calculated as follow.Hence the ratio of the masses will be,
$\dfrac{{m_1}}{{m_2}} = \dfrac{{{R^2}}}{{{r^2}}}$
Rearranging the above ratio we will get,
$m_1 = \dfrac{{{R^2}}}{{{r^2}}}m_2$
Putting equation $\left( 2 \right)$ in equation $\left( 1 \right)$ we will get,
$\dfrac{{{R^2}}}{{{r^2}}}m_2 - m_2 = m$
$ \Rightarrow m_2\left( {\dfrac{{{R^2}}}{{{r^2}}} - 1} \right) = m$
Hence on solving further we will get,
$m_2 = \dfrac{{m{r^2}}}{{{R^2} - {r^2}}}$