
A diatomic molecule is formed by two atoms which may be treated as mass points $m_1$ and $m_2$ joined by a massless rod of length r. Then, the moment of inertia of the molecule about an axis passing through the center of mass and perpendicular to rod is:
A. Zero
B. $({m_1} + m{}_2){r^2}$
C. $(\dfrac{{{m_1} + {m_2}}}{{{m_1}{m_2}}}){r^2}$
D. $(\dfrac{{{m^{_{}}}_1{m_2}}}{{{m_1} + {m_2}}}){r^2}$
Answer
597.3k+ views
Hint: for this we need to have basic knowledge of center of mass and moment of inertia. Moment of Inertia can be defined as how easily a body can be rotated about a given axis. It is a rotational analogue of mass.
Step by step solution:
1. Let us first draw a figure which will help us in better understanding of the Question.
Below we have drawn a rod AB where $m_1$ is the mass at point A and $m_2$ is the mass at point B. At point O we have assumed the center of mass of the rod. We have drawn a perpendicular axis to the rod about which moment of inertia is to be calculated. Let $r_1$ be the distance between point A and O and $r_2$ be the distance between point B and O.
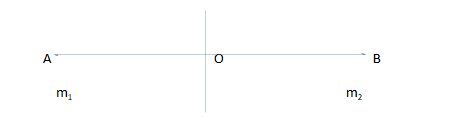
2. As we know that the position of center of mass of the particles is given by
$X = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + .......{m_n}{x_n}}}{{{m_1} + {m_2} + .....{m_n}}} = \dfrac{{\sum {{m_i}{x_i}} }}{{\sum {{m_i}} }}$ …………….equation 1
So here according to our figure we have ${r_1} = \dfrac{{{m_1} \times 0 + {m_2} \times r}}{{{m_1} + {m_2}}}$ because $m_1$ is at the 0 distance from point A and $m_2$ is at the distance r from point A.
Again ${r_1} = \dfrac{{{m_2} \times r}}{{{m_1} + {m_2}}}$ ………………equation 2
And ${r_2} = r - \dfrac{{{m_2} \times r}}{{{m_1} + {m_2}}}$ ……………..equation 3
3. Now Moment of Inertia is given by $I = {m_1}{x_1}^2 + {m_2}{x_2}^2 + .........{m_n}{x_n}^2$
Here in our question $I = {m_1}{r_1}^2 + {m_2}{r_2}^2$
With the help of equations 2 and 3 we get
$I = \dfrac{{{m_1}{m_2}^2{r^2}}}{{{{({m_1} + {m_2})}^2}}} + \dfrac{{{m_1}^2{m_2}{r^2}}}{{{{({m_1} + {m_2})}^2}}}$
Now taking some common terms
$I = \dfrac{{{m_1}{m_2}{r^2}}}{{{{({m_1} + {m_2})}^2}}}({m_1} + {m_2})$
After doing the simplifications we get:
$I = \dfrac{{{m_1}{m_2}{r^2}}}{{{m_1} + {m_2}}}$
Or it can also be written as $I = (\dfrac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}){r^2}$
Hence option D is correct.
Note: In this question basic knowledge of moment of inertia and simple algebra is used. We can also solve this type of question using numerical values instead of variables.
Step by step solution:
1. Let us first draw a figure which will help us in better understanding of the Question.
Below we have drawn a rod AB where $m_1$ is the mass at point A and $m_2$ is the mass at point B. At point O we have assumed the center of mass of the rod. We have drawn a perpendicular axis to the rod about which moment of inertia is to be calculated. Let $r_1$ be the distance between point A and O and $r_2$ be the distance between point B and O.
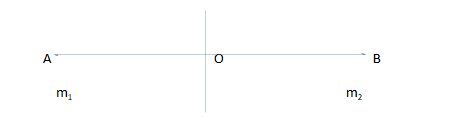
2. As we know that the position of center of mass of the particles is given by
$X = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + .......{m_n}{x_n}}}{{{m_1} + {m_2} + .....{m_n}}} = \dfrac{{\sum {{m_i}{x_i}} }}{{\sum {{m_i}} }}$ …………….equation 1
So here according to our figure we have ${r_1} = \dfrac{{{m_1} \times 0 + {m_2} \times r}}{{{m_1} + {m_2}}}$ because $m_1$ is at the 0 distance from point A and $m_2$ is at the distance r from point A.
Again ${r_1} = \dfrac{{{m_2} \times r}}{{{m_1} + {m_2}}}$ ………………equation 2
And ${r_2} = r - \dfrac{{{m_2} \times r}}{{{m_1} + {m_2}}}$ ……………..equation 3
3. Now Moment of Inertia is given by $I = {m_1}{x_1}^2 + {m_2}{x_2}^2 + .........{m_n}{x_n}^2$
Here in our question $I = {m_1}{r_1}^2 + {m_2}{r_2}^2$
With the help of equations 2 and 3 we get
$I = \dfrac{{{m_1}{m_2}^2{r^2}}}{{{{({m_1} + {m_2})}^2}}} + \dfrac{{{m_1}^2{m_2}{r^2}}}{{{{({m_1} + {m_2})}^2}}}$
Now taking some common terms
$I = \dfrac{{{m_1}{m_2}{r^2}}}{{{{({m_1} + {m_2})}^2}}}({m_1} + {m_2})$
After doing the simplifications we get:
$I = \dfrac{{{m_1}{m_2}{r^2}}}{{{m_1} + {m_2}}}$
Or it can also be written as $I = (\dfrac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}){r^2}$
Hence option D is correct.
Note: In this question basic knowledge of moment of inertia and simple algebra is used. We can also solve this type of question using numerical values instead of variables.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




