Question

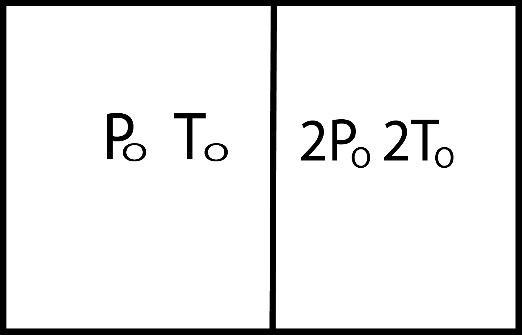
A diathermic piston divides adiabatic cylinder of volume $\,\,{V_o}\,$ into two equal parts as shown in the figure. Both the parts contain ideal monatomic gases. The initial pressure and temperature of gas in left compartment are $\,\,{P_o}\,$ and $\,\,{T_o}\,$ while that in right compartment are $\,2{P_o}\,$ and $\,\,2{T_o}\,$. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The pressure in left compartment after thermal equilibrium is achieved is:

A.$\,\,{P_o}\,\,$
B.$\,\,\dfrac{3}{2}{P_o}\,$
C.$\,\,\dfrac{4}{3}{P_o}\,$
D.None

Answer 1

Hint:A diathermic piston is a piston which allows transfer of heat but doesn’t allow transfer of matter. Again adiabatic means, a process in which no transfer of heat takes place. This does not mean that the temperature is constant, but rather that no heat is transferred into or out from the system. Equilibrium is a state of balance or a stable situation where opposing forces cancel each other out and no changes are occurring. The volume of the system is given. The initial pressure and temperature on both the compartments is mentioned . We have to find the final value after equilibrium is achieved.
Formulas used:
$\,\,{n_A} \times {C_v} \times \Delta {T_A} = {n_B} \times {C_v} \times \Delta {T_B}\,\,$
where, $\,\,{n_A}\,$ is the number of moles in the left compartment
$\,\,{n_B}\,$ is the number of moles in the right compartment
$\,\,{C_v}\,$ is the molar heat capacity when volume is constant, so the change in volume is zero.
$\,\,\Delta {T_A}\,$ is the change in temperature in the left compartment.
$\,\,\Delta {T_B}\,$ is the change in temperature in the right compartment.
$\,PV = nRT\,$ is another formula used here
where $\,P\,$ is pressure $\,V\,$ is volume $\,\,n\,$ is number of moles
$\,R\,$ is gas constant and $\,T\,$ is temperature.

Complete step by step answer:
Let us move into the calculations;
$\,\,\,{n_A} \times {C_v} \times \Delta {T_A} = {n_B} \times {C_v} \times \Delta {T_B}\,\,\,$
$\,\, \Rightarrow {n_A} \times {C_v} \times ({T_f} - {T_o}) = {n_B} \times {C_v} \times (2{T_o} - {T_f})\,\,$ ( Equation \[1\])
where, $\,\,{T_f}\,\,$ is final temperature and $\,\,{T_o}\,$ and $\,\,2{T_o}\,$ are the given temperatures in left compartment and right compartment respectively. Also ,$\,\,{T_o} < {T_f} < 2{T_o}\,$ .
Now $\,\,{C_v}\,$ from both sides gets cancelled.
$\,\,PV = {n_A}RT\,$ [ Now we substitute the values of all the variables of left compartment to find the value of the number of moles from left compartment]
$\,\, \Rightarrow {P_o}\dfrac{{{V_o}}}{2} = {n_A}R{T_o}\,$ (Equation \[2\])
[since it is said that volume $\,\,{V_o}\,$ is divided into two equal parts so each compartments volume is$\,\,\dfrac{{{V_o}}}{2}\,\,$]
$\,\, \Rightarrow {n_A} = \dfrac{{{P_o}{V_o}}}{{2RT}}\,\,$
Similarly, let’s calculate $\,{n_B}\,$
$\,\,PV = {n_B}RT\,\,$ [ Now we substitute the values of all the variables of right compartment to find the value of the number of moles from right compartment]
$\,\, \Rightarrow 2{P_o}\dfrac{{{V_o}}}{2} = {n_B}R2{T_o}\,\,$ (Equation \[3\])
[ the values are already given in the question]
$\,\, \Rightarrow {n_B} = \dfrac{{{P_o}{V_o}}}{{2RT}}\,\,$
Therefore, $\,\,{n_A} = {n_B}\,$
Now, putting this condition in equation $\,1\,$ , we can see that $\,\,{n_A}\,$and $\,\,{n_B}\,$also get cancelled, as they are the same.
So, we are left with $\,\,{T_f} - {T_o} = 2{T_o} - {T_f}\,$
$\,\, \Rightarrow 2{T_f} = 3{T_o}\,$
$\,\, \Rightarrow {T_f} = \dfrac{{3{T_o}}}{2}\,\,$
And according to, $\,\,PV = nRT\,$, we can say that $\,\,P\alpha T\,$, so
$\,\,\dfrac{{{P_o}}}{{{P_f}}} = \dfrac{{{T_o}}}{{{T_f}}}\,$
$\,\, \Rightarrow {P_f} = \dfrac{{{P_o}{T_f}}}{{{T_o}}}\,$, Now we substitute $\,\,{T_f} = \dfrac{{3{T_o}}}{2}\,$ and get $\,\,{P_f} = \dfrac{{3{P_o}}}{2}\,$
So, after equilibrium pressure will be equal on both sides so the correct answer is Option B $\,\,\dfrac{3}{2}{P_o}\,$.

Note:The above process is a detailed way of solving this question. There is also a shortcut method to solve this question. As we know we have to find the pressure at equilibrium, so to make it equal pressure in the left compartment will increase and that of the right compartment decreases because pressure in the left compartment is less than that of the pressure at the right compartment. So, we can simply just add the pressures of both the compartments and divide it by $\,\,2\,\,$. That is $\,\,\dfrac{{{P_o} + 2{P_o}}}{2} = \dfrac{{3{P_o}}}{2}\,$.