Question

A device $X$ is connected across an ac source of voltage $V = {V_0}\sin \omega t$ . The current through $X$ is given as $I = {I_0}\sin \left( {\omega t + \dfrac{\pi }{2}} \right)$.
(a) Identify the device $X$ and write the expression for its reactance.
(b) Draw graphs showing variation of voltage and current with time over one cycle of ac, for $X$ .
(c) How does the reactance of the device $X$ vary with frequency of the ac? Show this variation graphically.
(d) Draw the phasor diagram for the device $X$ .

Answer 1

Hint: Use the value of the current and the voltage given in the question, to find out the type of the device. Draw the graph of the current and voltage for that device. The reactance is inversely proportional to the frequency of the alternating current.

Useful formula:
The reactance of the capacitor is given as
$
{X_c} = \dfrac{1}{{\omega C}}$
Where ${X_c}$ is the reactance, $\omega = 2\pi f$ and it is the angular velocity and $C$ is the capacitance.


Complete step by step solution:
It is given that the
Source of voltage, $V = {V_0}\sin \omega t$
The current flowing through the $X$ is $I = {I_0}\sin \left( {\omega t + \dfrac{\pi }{2}} \right)$
(a) From the given data, it is clear that the current leads the voltage by $\dfrac{\pi }{2}$, so it must be the capacitor circuit. Hence its reactance is given as ${X_c} = \dfrac{1}{{\omega C}}$ .
(b)

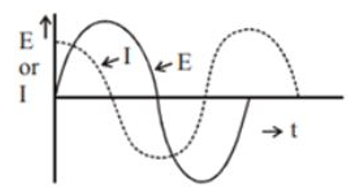
(c) From the result of the (a), ${X_c} = \dfrac{1}{{2\pi fC}}$, it is clear that the reactance is inversely proportional to the frequency.

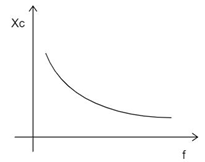
(d)

Note: There is a trick to find out the type of the device with its current value. If the current and the reactance is same, then it is resistor, if the current lags the voltage by $\dfrac{\pi }{2}$, it is inductance and if the current leads the voltage by the $\dfrac{\pi }{2}$, then the device is the capacitor.