
A dealer in the rural area wishes to purchase a number of sewing machines. He has only Rs. 5760 to invest and has spaces for at most 20 items for storage. An electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240. He can sell an electric machine at profit of Rs. 22 and a manually operated sewing machine at profit Rs. 18. Assuming that he can sell all the items that he can buy how should he invest his money in order to maximize his profit? Formulate this problem mathematically and then solve it.
Answer
533.1k+ views
Hint: In this problem, first we will formulate the objective function by the condition that a dealer can sell an electric machine at profit of Rs. 22 and a manually operated sewing machine at profit Rs. 18. After that we will formulate constraints by condition that he has only Rs. 5760 to invest and has spaces for at most 20 items for storage and an electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240. Then we will get objective function and constraints to formulate the LLP to maximize the profit of the dealer and then solve LLP using graphical methods.
Complete step by step answer:
Let x be the number of electronic sewing machines bought by the dealer and y be the number of electronic sewing machines bought by the dealer. Since the dealer can buy the which he can sell and the profit on the electronic sewing machine is Rs. 22 and profit on the manually sewing machine is Rs.18. let Z denotes the total profit on the sewing machines,
$\Rightarrow \text{Z}=22\text{x+18y}$
Since the dealers have at most 20 items to store.
$\Rightarrow \text{x+y}\le \text{20}$
Also, an electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240 and He has only Rs. 5760 to invest,
$\Rightarrow \text{360x+240y}\le 5760$
Dividing both sides by 120 in above inequation, we get
$\Rightarrow \text{3x+2y}\le 48$
Hence, from all above cases the LLP form to maximize the profit on the sewing machine is given below,
Maximize $\text{Z}=22\text{x+18y}$
Subject to
$\text{x+y}\le \text{20}$,
$\text{3x+2y}\le 48,\text{ }x>0,\text{ }y>0.$
Now by using graphical methods we will maximize the profit on sewing machines.
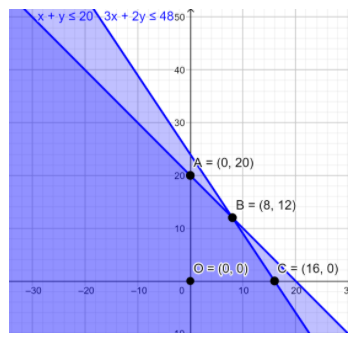
Hence the feasible region is region OABC.
We can compute point B by solving the equation $\text{x+y = 20}$ and $\text{3x+2y = }48.$
$\text{x+y = 20}....\text{(A)}$
$\text{3x+2y = }48....(B)$
Multiplying equation (A) by 3 and the subtracting from equation (B), we get
y =12.
Using y= 12 in equation (A), we get
x+12=20,
x=8.
From graph, A=(0, 20), O=(0, 0), C=(15, 0) and B=(8, 12) (coordinate of point B is verified in note).
Since the feasible region is bounded, therefore we will evaluate the value of Z at the boundaries of the region OABC.
From the table we get that B has a maximum value of Z.
Hence the dealer can buy 8 electronic sewing machines and 12 manually operated sewing machines.
Note: In this problem, one should know the feasible region bounded and unbounded. A solution which satisfies the constraints and non-negativity restriction is called feasible region. Try not to make any calculation mistakes while solving the problem.
Complete step by step answer:
Let x be the number of electronic sewing machines bought by the dealer and y be the number of electronic sewing machines bought by the dealer. Since the dealer can buy the which he can sell and the profit on the electronic sewing machine is Rs. 22 and profit on the manually sewing machine is Rs.18. let Z denotes the total profit on the sewing machines,
$\Rightarrow \text{Z}=22\text{x+18y}$
Since the dealers have at most 20 items to store.
$\Rightarrow \text{x+y}\le \text{20}$
Also, an electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240 and He has only Rs. 5760 to invest,
$\Rightarrow \text{360x+240y}\le 5760$
Dividing both sides by 120 in above inequation, we get
$\Rightarrow \text{3x+2y}\le 48$
Hence, from all above cases the LLP form to maximize the profit on the sewing machine is given below,
Maximize $\text{Z}=22\text{x+18y}$
Subject to
$\text{x+y}\le \text{20}$,
$\text{3x+2y}\le 48,\text{ }x>0,\text{ }y>0.$
Now by using graphical methods we will maximize the profit on sewing machines.

Hence the feasible region is region OABC.
We can compute point B by solving the equation $\text{x+y = 20}$ and $\text{3x+2y = }48.$
$\text{x+y = 20}....\text{(A)}$
$\text{3x+2y = }48....(B)$
Multiplying equation (A) by 3 and the subtracting from equation (B), we get
y =12.
Using y= 12 in equation (A), we get
x+12=20,
x=8.
From graph, A=(0, 20), O=(0, 0), C=(15, 0) and B=(8, 12) (coordinate of point B is verified in note).
Since the feasible region is bounded, therefore we will evaluate the value of Z at the boundaries of the region OABC.
| Corner Point | Z=22+X+18Y |
| O=(0,0) | Z=0 |
| A=(0,20) | Z=22(0)+18(20)=360 |
| B=(8,12) | Z=22(8)+18(12)=392 |
| C=(15,0) | Z=22(15)+18(10)=330 |
From the table we get that B has a maximum value of Z.
Hence the dealer can buy 8 electronic sewing machines and 12 manually operated sewing machines.
Note: In this problem, one should know the feasible region bounded and unbounded. A solution which satisfies the constraints and non-negativity restriction is called feasible region. Try not to make any calculation mistakes while solving the problem.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




