Question

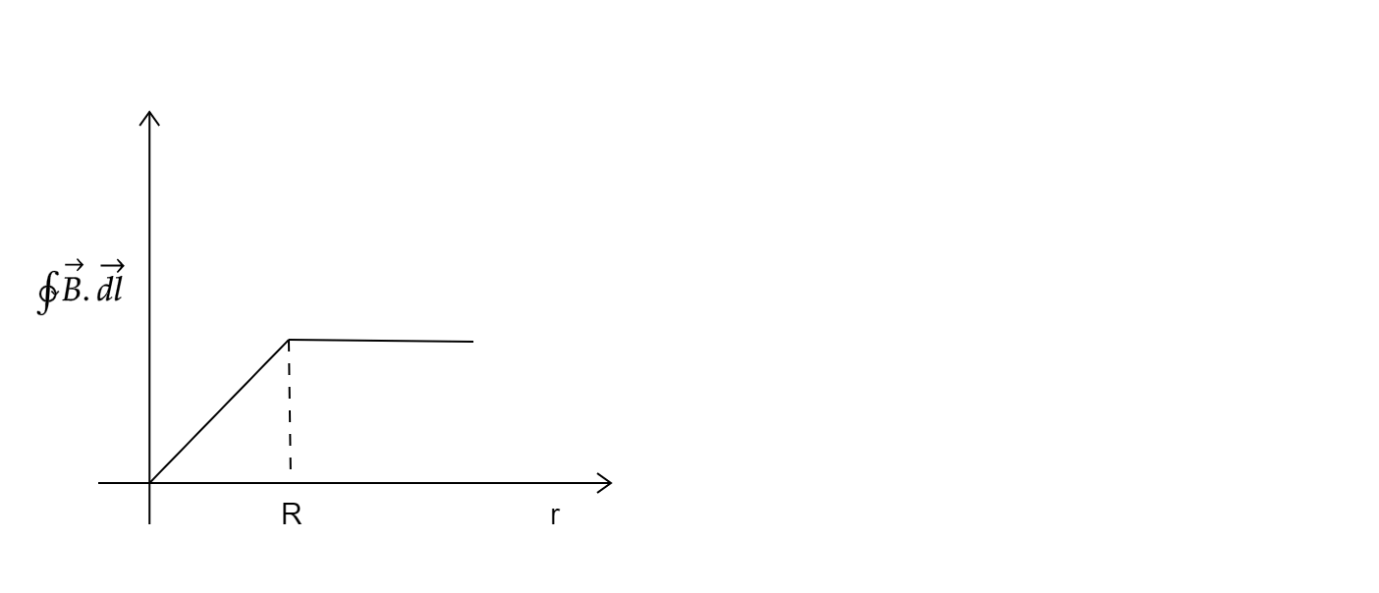
A cylindrical wire of radius $R$ is carrying a current $I$ uniformly distributed over its cross-section. If a loop of radius $r$ is taken as an amperian loop then the variation value of \[\oint {\overrightarrow B .\overrightarrow {dl} } \] over this loop with radius $r$ of loop will be best represented by-
A.

 B.

C.

D.

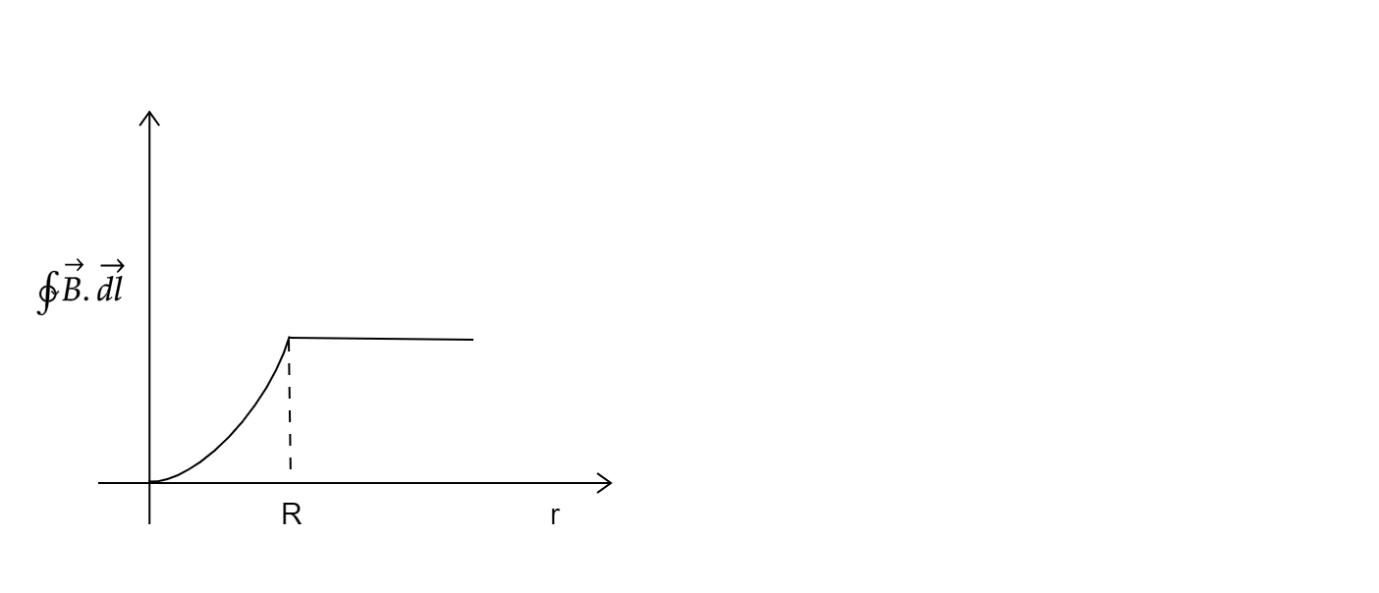
Answer 1

Hint: Find the current through the amperian loop by first taking amperian loop as smaller than $R$ and then by taking it bigger than $R$. Then by using ampere’s circuital law we can see the variation between \[\oint {\overrightarrow B .\overrightarrow {dl} } \] with respect to radiuses.

Complete answer:
We have been given graphs for \[\oint {\overrightarrow B .\overrightarrow {dl} } \] with respect to $R$ and $r$ where $R$ is the radius of the cylindrical wire and $r$ is the radius of the amperian loop
Using ampere circuital law,
\[\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}{I_{penetrating}}\]
Let's now see the cylindrical wire from its cross-sectional area side with radius $R$. Making an amperian loop inside it of radius $r$

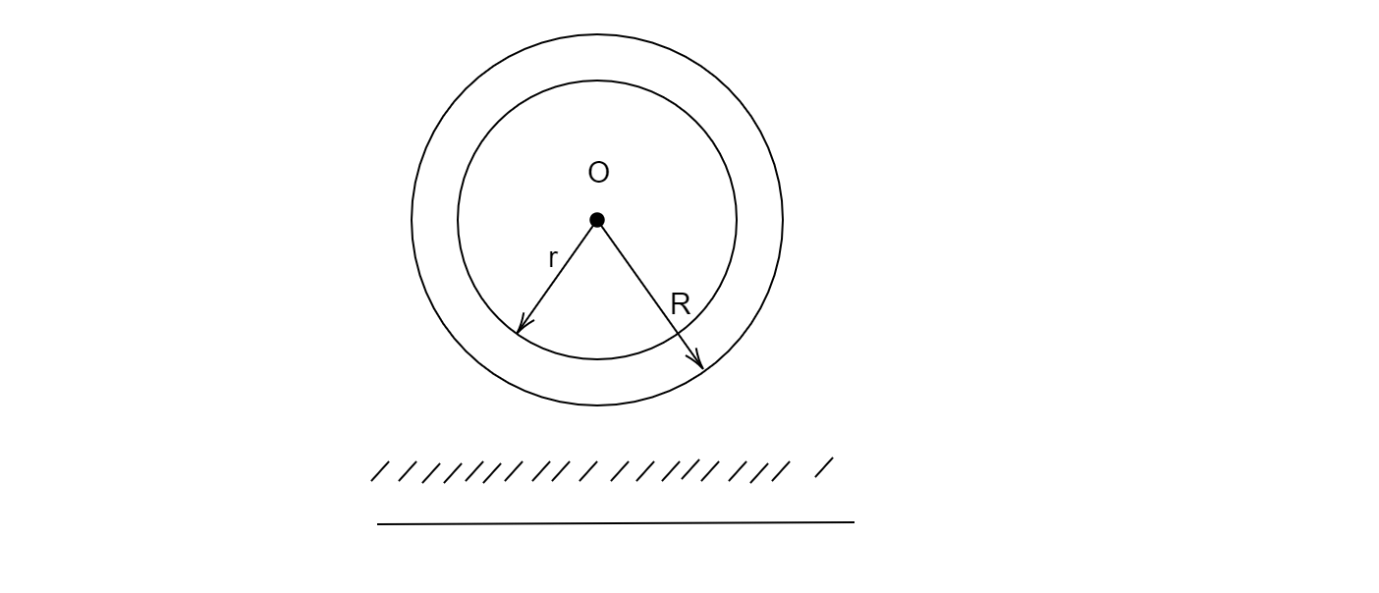
Finding the current density $J$ of this whole volume
\[J = \dfrac{I}{A}\] where $I$ is the current flowing through an area$A$
$ \Rightarrow I = JA$
For inside radius $r$
\[\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}(J\pi {r^2})\]
As for radius $R$ current density will be $J = \dfrac{I}{{\pi {R^2}}}$
Therefore, \[\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}(\pi {r^2}) \times \dfrac{I}{{\pi {R^2}}}\]
From this, we get that \[\oint {\overrightarrow B .\overrightarrow {dl} } \propto {r^2}\]
Now we will take an amperian loop that has a radius $r$ more than the radius $R$

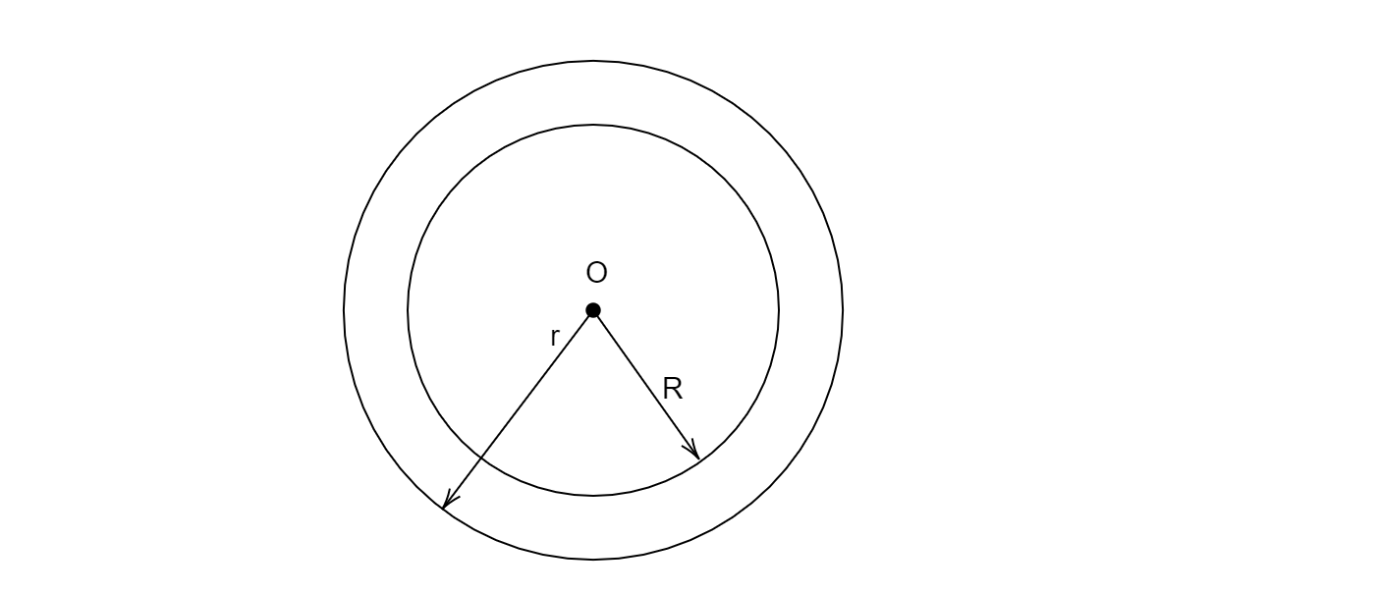
So for this outermost loop \[\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}I\]
For radius $R$
\[\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}(J\pi {R^2})\]
But The current is passing through the previous volume of wire only so for this also so the current density will be $J = \dfrac{I}{{\pi {R^2}}}$
So \[\oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}(\pi {R^2}) \times \dfrac{I}{{\pi {R^2}}}\]
\[ \Rightarrow \oint {\overrightarrow B .\overrightarrow {dl} } = {\mu _0}I\] is constant
So for $r < R$ , \[\oint {\overrightarrow B .\overrightarrow {dl} } \] is directly proportional to the square of the radius $r$
And for $r > R$ ,\[\oint {\overrightarrow B .\overrightarrow {dl} } \] is constant
This variation is shown by the graph given in option B

Hence option B) is the correct option.

Note:
The relationship between the current and the magnetic field induced by it is described by Ampere's Circuital Law. The product of current confined by the path and permeability of the medium equals the integral of magnetic field density along an imagined closed path, according to this law.