Question

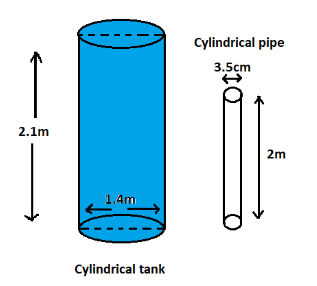
A cylindrical water tank of diameter 1.4m and height 2.1m is being fed by a pipe of diameter 3.5cm through which water flows at the rate of 2m/s. Calculate the time (in minutes) it takes to fill the tank.

Answer 1

Hint: Find the volume of the cylindrical water tank. The pipe is also in cylinder shape. We are given the speed of water. Speed is the ratio of distance to time. Therefore the height of the cylindrical pipe will be 2. Find the volume of the cylindrical pipe. To get the time it takes to fill the tank divide the volume of the tank with the volume of pipe.
Volume of a cylinder is $ \pi {r^2}h $ , where r is the base radius, h is the height of the cylinder and the value of $ \pi = \dfrac{{22}}{7} $

Complete step-by-step answer:
We are given that a cylindrical water tank of 1.4m and height 2.1m is being fed by a pipe of diameter 3.5cm through which water flows at the rate of 2m/s.
We have to calculate the time taken by the pipe to fill the tank in minutes.

Volume of the cylindrical tank is $ \pi {r^2}h $
Diameter is 1.4m. Radius is half the diameter. Therefore, the radius of the tank is 0.7m and the height is 2.1m.
1 meter is equal to 100 centimeters.
0.7m is 70cm and 2.1 m is 210 cm.
 $
  Volum{e_{tank}} = \pi {r^2}h \\
  r = 70cm,h = 210cm \\
   \Rightarrow Volum{e_{tank}} = \dfrac{{22}}{7} \times 70 \times 70 \times 210 \\
   \Rightarrow Volum{e_{tank}} = 3234000c{m^3} \\
  $
Volume of the cylindrical pipe is $ \pi {r^2}h $
The diameter of the pipe is 3.5cm.
We are given the speed of water which is 2m/s. Therefore the height (distance) of the pipe is 2m, which is 200cm.
 $
  Volum{e_{pipe}} = \pi {r^2}h \\
  r = \dfrac{{3.5}}{2}cm,h = 200cm \\
   \Rightarrow Volum{e_{pipe}} = \dfrac{{22}}{7} \times \dfrac{{3.5}}{2} \times \dfrac{{3.5}}{2} \times 200 \\
  \therefore Volum{e_{pipe}} = 1925c{m^3} \\
  $
Divide the volume of the tank with the volume of pipe to get the time it takes to fill the tank.
 $
  Time = \dfrac{{Volum{e_{tank}}}}{{Volum{e_{pipe}}}} \\
   \Rightarrow Time = \dfrac{{3234000}}{{1925}}\sec \\
  \therefore Time = 1680\sec \\
  $
1 minute is 60 seconds, how many minutes is 1680 seconds
 $ \dfrac{{1680}}{{60}} = 28minutes $
Therefore, the time taken by the pipe to fill the tank is 28 minutes.

Note: When we divided the volume of the tank with the volume of pipe, we considered the result in seconds, because the rate of water flow is given in seconds. So the time will be resulting in seconds. Speed is the distance by time and the given speed is 2m/s, 2 metres per one second. In one second, the water travels 2 metres, therefore the length of the pipe must be considered as 2 metres.