Question

A cylindrical vessel is filled with the water as shown in figure. A hole should be bored so that the water comes out upto maximum distance of:

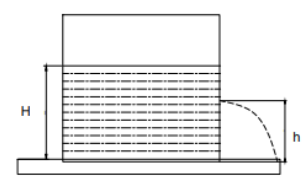
A. $\dfrac{{3H}}{4}\,from\,surface$
B. $\dfrac{H}{4}\,from\,surface$
C. $H\,from\,surface$
D. $\dfrac{H}{2}\,from\,surface$

Answer 1

Hint: The different position of the hole will decide the different velocity of water coming out of the vessel. It is given in the question that the hole should be made such that water falls at maximum distance from the vessel.

Formula used:
We can use the formula of velocity
$v = \sqrt {2gh} $
Here, $h$ is the height from the surface, $v$ is the velocity of water and $g$ is the acceleration due to gravity.

Complete step by step answer:
Suppose that we have to drill a hole at the depth h from the surface of liquid. Then, we will have the velocity of water coming out of the vessel as
 $ v = \sqrt {2gh} $
Consider that the liquid will take time ‘t’ to reach the distance x from the base of the vessel.Considering this vertical motion of ejected liquid we have the equation
$H - h = \left( {\dfrac{1}{2}g{t^2}} \right)$
We can rearrange this equation and get in terms of time as
$t = \sqrt {\dfrac{{2(H - h)}}{g}} $
Similarly if we consider the horizontal motion we will get,
$x = vt \\
\Rightarrow t\sqrt {2gh} ....(v = \sqrt {2gh} ) \\ $
Now substituting the time value already obtained in this equation we get
${x^2} = 2gh{t^2} \\
\Rightarrow 2gh\left( {\dfrac{{2(H - h)}}{g}} \right) \\
\Rightarrow 4h(H - h)...(i) \\ $
Now for the maximum value of $x$ we can differentiate the value of $ {x^2}$ and equate it to zero. This is the method of finding maximum and minimum value conditions.
$ \dfrac{{d({x^2})}}{{dh}} = \dfrac{d}{{dh}}\left( {4h(H - h)} \right) \\
\Rightarrow 4(H - 2h) \\ $
If we equate the outcome to zero we will get the required condition
$4(H - 2h) = 0 \\
\Rightarrow H = 2h \\
\Rightarrow h = \dfrac{H}{2}$
So, we need to bore a hole at a distance $ \dfrac{H}{2}\,$ from the surface.

Hence, option D is correct.

Note: The efflux changes as we go on drilling the holes at different heights from the surface. This change in efflux is seen due to its dependence on the height. This is often termed as Torricelli's Law. Torricelli’s law has practical applications in daily life. The physical law describes a major relationship between liquid exit velocity and its height in the container.