Question

A cylindrical vessel 60 cm in diameter is partially filled with water. A sphere, 54 cm in diameter is gently dropped into the vessel. To what further height will the water rise in the cylinder?
A. 20.02 cm
B. 30.29 cm
C. 29.16 cm
D. 25 cm

Answer 1

Hint: This is a problem of mensuration and requires the concept of volumes of 3-D objects. We will assume that the sphere is completely submerged in the water. The volumes of cylinders and spheres can be obtained by the formulas-
${{\text{V}}_{cylinder}} = \pi {r^2}{\text{h where r is radius and h is height}}$
${{\text{V}}_{sphere}} = \dfrac{4}{3}\pi {r^3}\; \text{where r is radius}$

Complete step-by-step solution -
Let us assume that the water is initially filled up to a height h. When we add the sphere, let the level of water increase to a height $(h + x)$ as-

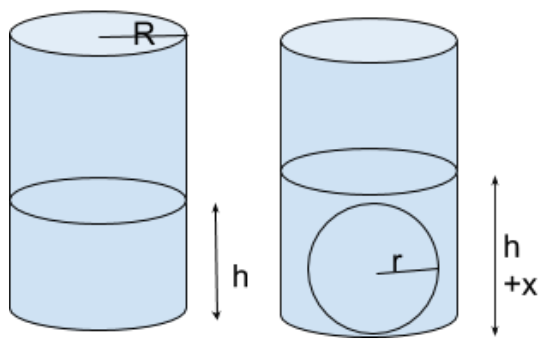
Let the radius of the cylinder be R and that of the sphere be r. We have been given their diameters. To find their respective radii, we can proceed as-
${\text{R}} = \dfrac{{\text{D}}}{2} = \dfrac{{60}}{2} = 30\;cm$
${\text{r}} = \dfrac{{\text{d}}}{2} = \dfrac{{54}}{2} = 27\;cm$
The initial volume of water in the cylinder can be calculated using the formula as-
$\pi {R^2}{\text{h}}$
The volume of sphere in the vessel is-
$\dfrac{4}{3}\pi {r^3}$
After adding the sphere, the height of the water increases by a length x cm, so we can form the equation that-
Initial volume of water + Volume of sphere = Final volume of water
$\begin{align}
  &\pi {R^2}{\text{h}} + \dfrac{4}{3}\pi {r^3} = \pi {R^2}\left( {{\text{h}} + {\text{x}}} \right) \\
  &The\;{{\pi }}\; \text{term is common an can be cancelled} - \\
  \Rightarrow &{{\text{R}}^2}{\text{h}} + \dfrac{4}{3}{{\text{r}}^3} = {{\text{R}}^2}\left( {{\text{h}} + {\text{x}}} \right) \\
   \Rightarrow &\dfrac{4}{3}{{\text{r}}^3} = {{\text{R}}^2}{\text{h}} + {{\text{R}}^2}{\text{x}} - {{\text{R}}^2}{\text{h}} \\
  \Rightarrow &\dfrac{4}{3}{{\text{r}}^3} = {{\text{R}}^2}{\text{x}} \\
 \Rightarrow &Applying\;{\text{R}}\; = \;30\;cm\;and\;{\text{r}}\; = \;27\;cm\; \\
  \Rightarrow &\dfrac{4}{3}{\left( {27} \right)^3} = {30^2}{\text{x}} \\
 \Rightarrow &{\text{x}} = 29.16\;cm \\
\end{align} $
This is the increase in height. The correct option is C.

Note: In this question, it may seem confusing that we are assuming two variables h and x, and forming just one equation. But on further simplification, we can see that the variable ‘h’ is eliminated and the only x is left, which can be solved. Also, we should not forget to write the units in the final answer and always make a relevant diagram in questions related to mensuration.