Question

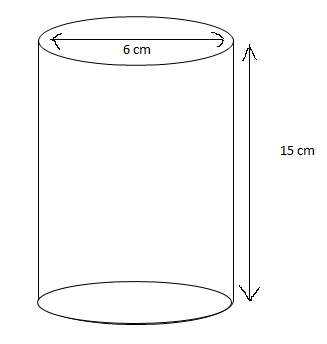
A cylindrical container of radius $6cm$ and height $15cm$ is filled with the ice cream. The whole ice cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is four times the radius of its base, find the radius of the ice cream cone.

Answer 1

Hint: Proceed the solution by finding the Volume of cone with hemispherical top. Volume of cone with hemispherical top = volume of cone $ + $volume of hemispherical top.

Complete step-by-step answer:
Let us consider the radius of base of the conical portion be $r$ cm
And given height of conical portion =$4rcm$

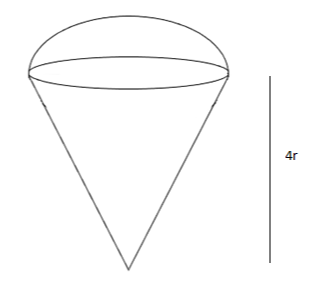
Now let us find the volume of cone with hemispherical top, it is nothing but a combination of cone and hemisphere.
So,
Volume of cone with hemispherical top=volume of cone$ + $volume of hemispherical top
We know that volume of cone=$\dfrac{1}{3}\pi {r^2}h$
And volume of hemispherical top=$\dfrac{2}{3}\pi {r^3}$
Therefore,
Volume of cone with hemispherical top = $\dfrac{1}{3}\pi {r^2}h$$ + $$\dfrac{2}{3}\pi {r^3}$
                                                                =$\left( {\dfrac{1}{3}\pi {r^2} \times 4r+\dfrac{2}{3}\pi {r^3}} \right)c{m^3}$
     Since height of conical portion (h) = $4rcm$(from given data)
                                                                = $\left( {\dfrac{6}{3}\pi {r^3}} \right)c{m^3}$
                                                                =$2\pi {r^3}c{m^3}$
$\therefore $ Volume of cone with hemispherical top=$2\pi {r^3}c{m^3}$
Then volume of $10$ cone with hemispherical top = $10$$ \times $$2\pi {r^3}c{m^3}$
$\therefore $ Volume of $10$ cone with hemispherical top = $20\pi {r^3}c{m^3}$
We know that volume of cylinder =$\pi {r^2}h$
Given radius of cylindrical container = $6cm$and height of the cylindrical container is 15 cm.
$\therefore $ Volume of cylindrical container =$\pi \times 6 \times 6 \times 15 = 540\pi c{m^3}$
Clearly they mentioned that
Volume of $10$ cone with hemispherical top = Volume of cylindrical container
$
   \Rightarrow 20\pi {r^3} = 540\pi \\
   \Rightarrow r = 3cm \\
 $
Therefore the radius of ice cream is =$3cm$
Note: Here after finding the volume of cones with hemispherical top we have to find Volume of $10$ cones with hemispherical top.