Question

A cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is four times the radius of its base, find the radius of the ice-cream cone.
(a) 3 cm
(b) 1 cm
(c) 4 cm
(d) 2 cm

Answer 1

Hint: Assume the radius and height of the cylinder as $R\text{ and }H$ respectively. Also, assume the radius of cone and hemispherical top as $r$ and height of cone as $h$. Use the relation: volume of cylinder is equal to 10 times the volume of sum of cone and hemisphere. Substitute all the given values and find the value of $r$.

Complete step-by-step answer:

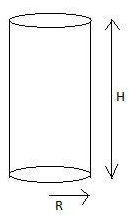
Let us assume that radius and height of cylinder as $R\text{ and }H$ respectively and height of cone be $h$. Since, the hemisphere of ice-cream is to be surmounted on the cone, therefore, the radius of cone and hemisphere should be equal. Let us assume that $r$.

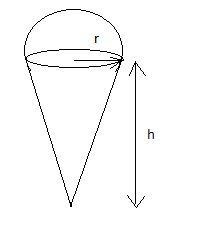
Now, since the total volume of ice-cream in the cylinder remains constant after distribution. Therefore,
$\begin{align}
  & \text{volume of cylinder}=10\times \left( \text{volume of cone}+\text{volume of hemisphere} \right) \\
 & \Rightarrow \pi {{R}^{2}}H=10\times \left( \dfrac{1}{3}\pi {{r}^{2}}h+\dfrac{2}{3}\pi {{r}^{3}} \right) \\
\end{align}$
It is given to us that, height of the conical portion is four times the radius of its base. Therefore, mathematically, $h=4r$. Therefore, the volume relation becomes,
$\begin{align}
  & \pi {{R}^{2}}H=10\times \left( \dfrac{1}{3}\pi {{r}^{2}}\times 4r+\dfrac{2}{3}\pi {{r}^{3}} \right) \\
 & \pi {{R}^{2}}H=10\times \left( \dfrac{4}{3}\pi {{r}^{3}}+\dfrac{2}{3}\pi {{r}^{3}} \right) \\
 & \pi {{R}^{2}}H=10\times \left( \dfrac{6}{3}\pi {{r}^{3}} \right) \\
 & \pi {{R}^{2}}H=10\times \left( 2\pi {{r}^{3}} \right) \\
\end{align}$
Now, substituting $R=6\text{ and }H=15$, we get,
$\begin{align}
  & \pi \times {{6}^{2}}\times 15=10\times 2\times \pi {{r}^{3}} \\
 & \Rightarrow {{r}^{3}}=\dfrac{\pi \times {{6}^{2}}\times 15}{10\times 2\times \pi } \\
\end{align}$
Cancelling the common terms we get,
$\begin{align}
  & \Rightarrow {{r}^{3}}=3\times 3\times 3 \\
 & \Rightarrow {{r}^{3}}={{3}^{3}} \\
 & \Rightarrow r=3 \\
\end{align}$
Therefore, the radius of the cone is 3 cm.
Hence, option (a) is the correct answer.

Note: One may note that we have used the volume relation to solve the question. This is because when the cylindrical container containing ice-cream will be distributed equally among 10 children then the total volume will remain the same before and after distribution. Never use area relation as it will be the wrong approach.