Question

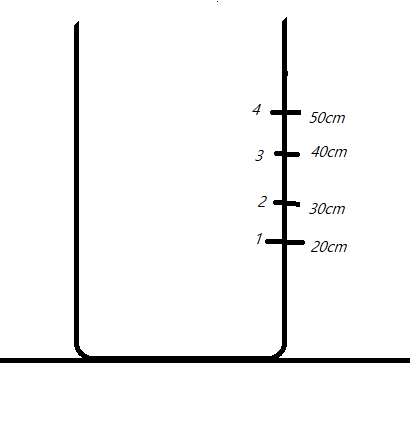
A cylinder vessel of height \[90cm\] is kept filed up to the brim. It has four holes \[1,2,3\text{ and 4}\] which are, respectively, at height of \[20cm,30cm,40cm\text{ and }50cm\] from the horizontal floor. The water at the maximum horizontal distance from the vessel comes from: (Note: this question has multiple correct answers)
 

A. hole $4$
B. hole $3$
C. hole $2$
D. hole $1$

Answer 1

Hint: The water falling from the hole, at a horizontal height from the ground follows a trajectory. Then we know that the horizontal distance covered by the water is given by $x=2\sqrt {h(H-h)}$. Using the given data and the formula we can find the height at which range is maximum.

Formula used:
$x=2\sqrt {h(H-h)}$

Complete step by step answer:
Given that the water from a tank of height $H=90cm$ flows through the holes \[20cm,30cm,40cm\text{ and }50cm\].
Then the vertical distance travelled by the water is given by $H-h=\dfrac{1}{2}gt^{2}$. Rearranging we get $t=\sqrt{\dfrac{2(H-h)}{g}}$. The water from the hole $h$ flows at a velocity $v=\sqrt{2gh}$. The water travels along the x-axis during the same time$t$is given by $x=vt$. Substituting, we get, $x=\sqrt{2gh}\sqrt{\dfrac{2(H-h)}{g}}=2\sqrt {h(H-h)}$
Then the maximum range is given by $x=2\sqrt {h(H-h)}$.
To find the maximum range at $hole\; 1=20cm$, substituting the given values, we get$x=2\sqrt{20(90-20)}=2\sqrt{20\times 70}=2\sqrt{140}=23.66cm$
For $hole\; 2=30cm$,substituting the given values, we get $x=2\sqrt{30(90-30)}=2\sqrt{30\times 60}=2\sqrt{180}=6\sqrt{20}=26.83cm$
For $hole\; 3=40cm$,substituting the given values, we get $x=2\sqrt{40(90-40)}=2\sqrt{40\times 50}=2\sqrt{2000}=89.44cm$
For $hole\; 4=50cm$,substituting the given values, we get$x=2\sqrt{50(90-50)}=2\sqrt{50\times 40}=2\sqrt{2000}=89.44cm$
Thus clearly, at hole $4$ and hole $3$ the range is maximum.
Another way to understand this answer is, maximum range occurs at $R_{max}=\dfrac{H}{2}$, here since $H=90cm$ then $R_{max}=\dfrac{90}{2}=45cm$, which is a value between at hole $4$ and hole $3$ . Thus , the answer is hole $4$ and hole $3$ .
Hence the answer is A. hole $4$ and B. hole $3$

Note:
This sum is a variant of the projectile motion. Generally, in the projectile motion sums, the body starts from the x-axis, travels along the y-axis and reaches the x-axis again. But here the water starts from the y-axis, from the maximum height. We need to find the maximum range, which water reaches.