Question

A cylinder tank full of water is emptied by a pipe at the rate of \[225\,liters\,{\min ^{ - 1}}\]. How much time will it take to empty half the tank, if the diameter of its base is \[3m\] and its height is \[3.5m\]? (use \[\pi = \dfrac{{22}}{7}\])

Answer 1

Hint: To solve this question first we assume a variable as the volume of the cylinder. Then we find the volume of the cylinder by using the formula by putting the value of radius and height. After that, we take only half the volume and convert it into liters. Then we calculate the time taken to empty half of the tank.

Complete step-by-step solution:

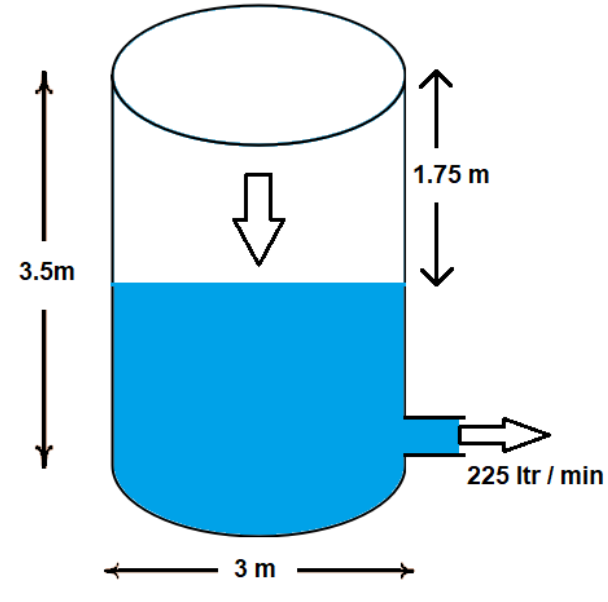
Given,
Water is emptied by the rate of \[225\,liters\,{\min ^{ - 1}}\] from a cylindrical tank.
The diameter of the base of the cylinder is \[3m\]
Radius of the cylinder is \[r = 1.5\]
Height of the cylinder is \[h = 3.5m\]
To find,
Time is taken to empty half the tank.
The volume of water stored in a cylindrical tank is equal to the total volume of the cylinder.
Let, the volume of the cylinder is \[v\].
Formula of volume of cylinder is-
\[ \Rightarrow v = \pi {r^2}h\]
Here, \[r\] is the radius of the cylinder,
\[h\] is the height of the cylinder
On putting the values of height and radius
\[v = \pi {\left( {1.5} \right)^2} \times 3.5\]
On solving square part
\[v = \pi \times 2.25 \times 3.5\]
On putting the value of \[\pi \]
\[v = \dfrac{{22}}{7} \times 2.25 \times 3.5\]
On further calculations
\[v = 22 \times 2.25 \times 0.5\]
On further solving
\[v = 24.75{m^3}\]
We have to calculate time for half volume
\[\dfrac{v}{2} = \dfrac{{24.75}}{2}{m^3}\]
Half volume \[\dfrac{v}{2} = 12.375{m^3}\]
Now convert this volume in liters
To convert in liters we have to multiply by 1000
\[\text{Total volume} = 12.375 \times 1000litres\]
Onn further calculation
\[\text{Total volume} = 12375litres\]
Time taken to empty half a tank is the ratio of volume to the rate of empty.
\[\text{Time taken} = \dfrac{{volume}}{{speed}}\]
On putting the values:
\[\text{Time taken} = \dfrac{{12375}}{{225}}\min \]
On further calculations:
\[\text{Time taken} = 55\min \]
Final answer:
Time taken to empty half tank is
\[\text{Time taken} = 55\min \]

Note: Students commit mistakes in concluding the volume of the cylinder and the total water volume are equal. They usually forget to take half volume because we have to conclude time to empty only half tank and forget to convert the volume in liters because speed is given in liters per minute.