Question

A cyclist riding a bicycle at a speed of $14\sqrt{3}\;ms^{-1}$ takes a turn around a circular road of radius $20\sqrt{3}\;m$ without skidding. What is his inclination to the vertical?
A. $30^{\circ}$
B. $45^{\circ}$
C. $60^{\circ}$
D. $75^{\circ}$

Answer 1

Hint: Sketch out a diagram illustrating all the forces that the cyclist is subjected to. Account for the normal reaction force and its components, the gravitational force, and the centrifugal force that the cyclist experiences as he takes a turn around the bend. Following this, determine the expressions for forces at equilibrium and numerically solve them to arrive at a relation for the angle of inclination, following which you can just plug in the given values and obtain the appropriate result.

Formula Used:
Angle of inclination $\theta = tan^{-1}\left(\dfrac{v^2}{rg}\right)$

Complete step by step answer:
As the cyclist takes a turn around the circular road, he bends at a certain angle in order to balance his weight on the bicycle. This leads to an exertion of a normal reaction by the road on the bicycle. Let the inclination of the cyclist be $\theta$ with the vertical. He also experiences a centrifugal force directed away from the bend. At equilibrium, all these forces come together to prevent the cyclist from skidding across the road:
$Nsin\theta = \dfrac{mv^2}{r}$
$Ncos\theta = mg$

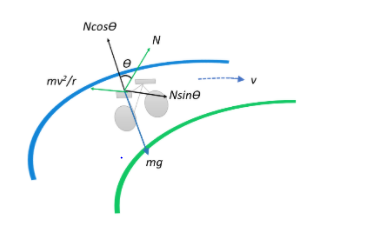
Dividing the two equations we get:
$tan\theta = \dfrac{v^2}{rg} \Rightarrow \theta = tan^{-1}\left(\dfrac{v^2}{rg}\right)$
Given that $v=14\sqrt{3}\;ms^{-1}$, $r= 20\sqrt{3}\;m$ and $g=9.8\;ms^{-2}$
$\Rightarrow \theta = tan^{-1}\left(\dfrac{(14\sqrt{3})^2}{10\sqrt{3} \times 9.8}\right) = tan^{-1}\left(\dfrac{196 \times 3}{196 \times \sqrt{3}}\right) = tan^{-1}\left(\dfrac{3}{\sqrt{3}}\right)$
$\Rightarrow \theta = tan^{-1}(\sqrt{3}) = 60^{\circ}$
Therefore, the correct choice would be C. $ 60^{\circ}$

Note:
It is always essential to deduce which component of the forces are acting in which direction. By resolving our influencing forces to their respective components, we are able to isolate only those components of forces that contribute to the equilibrium of the body in that direction. Also ensure that the subsequent inclination angle that you obtain is the angle of the normal reaction with the vertical and not the horizontal or in general, as the question specifies.