Question

A cyclic quadrilateral ABCD of area $\dfrac{{3\sqrt 3 }}{4}$ is inscribed in a unit circle. If one of its sides AB =$1$ and diagonal BD=$\sqrt 3 $, find the lengths of the other sides.

Answer 1

Hint:Area of the quadrilateral is the sum of the areas of the two triangles which are separated by diagonal BD. Use cosine rule and sine rule of the triangle in both the triangles to evaluate the sides of the quadrilateral.

Complete step-by-step answer:
First, we draw the figure using the given information.

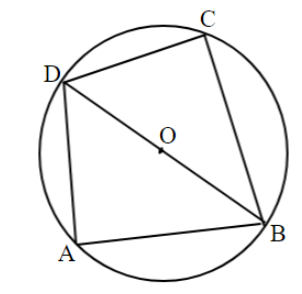
We are given that one of its sides AB =$1$ and diagonal BD=$\sqrt 3 $.
We have to find the length of other sides.
Since, O is the centre of the circles therefore radii OA=OB=OC=OD =$1$.
First, we find the measure of $\angle A$.
Use the formula of sine rule for circumcircle radius that is,
$\dfrac{{BD}}{{\sin A}} = 2R$
here $R$ is the radius of the circumcircle.
Substitute all the values and find $\angle A$.
$
  \dfrac{{\sqrt 3 }}{{\sin A}} = 1 \\
   \Rightarrow \sin A = \dfrac{1}{{\sqrt 3 }} \\
  \therefore A = 60^\circ \\
 $
Since the sum of opposite angles of cyclic quadrilateral is $180^\circ $ therefore, $\angle C = 120^\circ $
Now, we use cosine rule in $\Delta ABD$
$\cos A = \dfrac{{A{B^2} + A{D^2} - B{D^2}}}{{2ABAD}}$
Substitute all the values.
\[\cos 60^\circ = \dfrac{{1 + A{D^2} - 3}}{{2AD}}\]
Substitute $\cos 60^\circ = \dfrac{1}{2}$ and cross multiply to solve the equation.
\[
   \Rightarrow \dfrac{1}{2} = \dfrac{{1 + A{D^2} - 3}}{{2AD}} \\
   \Rightarrow A{D^2} - AD - 2 = 0 \\
 \]
Solve the quadratic equation and discard the negative value of AD.
$
  A{D^2} - 2AD + AD - 2 = 0 \\
   \Rightarrow AD(AD - 2) + 1(AD - 2) = 0 \\
   \Rightarrow (AD - 2)(AD + 1) = 0 \\
  \therefore AD = 2 \\
    \\
 $
Now, we use cosine rule in $\Delta BCD$
$\cos C = \dfrac{{B{C^2} + C{D^2} - B{D^2}}}{{2BCDC}}$
Substitute all the values.
\[\cos 120^\circ = \dfrac{{B{C^2} + C{D^2} - 3}}{{2(BC)(CD)}}\]
Substitute $\cos 120^\circ = \dfrac{{ - 1}}{2}$ and cross multiply to solve the equation.
\[
   \Rightarrow - \dfrac{1}{2} = \dfrac{{B{C^2} + C{D^2} - 3}}{{2(BC)(CD)}} \\
   \Rightarrow B{C^2} + C{D^2} + (BC)(CD) - 3 = 0.....(1) \\
 \]
We are given a cyclic quadrilateral ABCD of area $\dfrac{{3\sqrt 3 }}{4}$.
Therefore,
Area of cyclic quadrilateral = Area of $\Delta ABC$+ Area of $\Delta BCD$
Write the area of the triangle using the formula $\dfrac{1}{2}ab\sin \theta $, here $\theta $ is the angle between the side lengths $a$and $b$.
Write the areas in the mathematical form using the above result.
\[\dfrac{{3\sqrt 3 }}{4} = \dfrac{1}{2} \times 1 \times 2 \times \sin 60^\circ + \dfrac{1}{2} \times BC \times CD \times \sin 120^\circ \]
Substitute $\sin \,60^\circ = \sin 120^\circ = \dfrac{1}{2}$and cross multiply to solve the equation.
\[
   \Rightarrow \dfrac{{3\sqrt 3 }}{4} = \dfrac{1}{2} \times 1 \times 2 \times \dfrac{1}{{\sqrt 3 }} + \dfrac{1}{2} \times BC \times CD \times \dfrac{1}{{\sqrt 3 }} \\
   \Rightarrow 2 + BC \times CD = 3 \\
   \Rightarrow BC \times CD = 1.........(2) \\
 \]
Substitute the value of $BC \times CD$ in the equation $(1)$.
\[
  \therefore B{C^2} + C{D^2} + 1 - 3 = 0 \\
   \Rightarrow B{C^2} + C{D^2} = 2..............(3) \\
 \]
From equation $(2)$and $(3)$,the only possible value of $BC$and $CD$ is $1$.
Therefore, the length of the other sides is $AD = 1$ and $BC = CD = 1$

Note:Use the sine and cosine rule of the triangle by analysing the angle and the side which includes in the rule properly.
If the length of the sides of the cyclic quadrilateral is $a,b,c$ and $d$ then the area of the cyclic quadrilateral will be
$\sqrt {(s - a)(s - b)(s - c)(s - d)} $
Here, $s = \dfrac{{a + b + c + d}}{2}$