Question

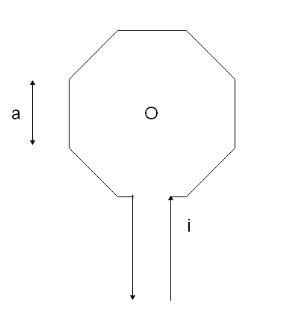
A current $ I $ is flowing in an octagonal coil of side $ a $ as shown in the figure. The magnetic field induction at the centre O of the coil will be
A) $ \dfrac{{5{\mu _0}I}}{{4\pi a}} $
B) $ \dfrac{{5\sqrt 2 {\mu _0}I}}{{\pi a}} $
C) $ \dfrac{{{\mu _0}I}}{{\sqrt 5 \pi a}} $
D) $ \dfrac{{\sqrt 5 {\mu _0}I}}{{2\pi a}} $

Answer 1

Hint : We will break the octagon down into 8 finite current-carrying cables instead of measuring the field due to an octagon. Then we will calculate the net magnetic field at the centre of the octagon due to these 8 currents carrying cables.

Formula used: In this question, we will use the following formula:
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi l}}(\sin {\phi _1} + \sin {\phi _2}) $ where $ B $ is the magnetic field generated by a current-carrying cable at a point that is a distance $ l $ away from the wire and subtends angles $ {\phi _1} $ and $ {\phi _2} $ with respect to the line perpendicular to the current-carrying cable.

Complete step by step answer
We’ve been given a current-carrying octagon and have been asked to find the magnetic field at the center of the octagon. Let us break the octagon down into 8 finite straight current-carrying cables that will exert an equal amount of magnetic field at the center of the coil. Then we can find the magnetic field due to one of these cables using the formula
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi l}}(\sin {\phi _1} + \sin {\phi _2}) $
The angle subtended by one of the sides of the octagon at the centre of the octagon will be equal to,
 $\Rightarrow \phi = \dfrac{{360}}{{{\text{number of sides of octagon}}}} $
 $ \Rightarrow \phi = \dfrac{{360}}{8} = 45^\circ $
Since we have a regular octagon the angle subtended by the two ends of the line with respect to the line perpendicular to the side will have the values,
 $\Rightarrow {\phi _1} = {\phi _2} = \dfrac{\phi }{2} $
 $ \Rightarrow {\phi _1} = {\phi _2} = 22.5^\circ $
To determine the perpendicular distance between the side and the point, we use the tangent of the angle $ {\phi _1} $ as,
 $\Rightarrow \tan {\phi _1} = \dfrac{{a/2}}{l} $
 $ \Rightarrow l = \dfrac{a}{{2 \times \tan 22.5^\circ }} $
Substituting the values of $ {\phi _1} = {\phi _2} = 22.5^\circ $ and $ l = \dfrac{a}{{2 \times \tan 22.5^\circ }} $ , we can calculate the magnetic field as
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi \dfrac{a}{{2 \times \tan 22.5^\circ }}}}(\sin 22.5^\circ + \sin 22.5^\circ ) $
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi a}}(4 \times \tan 22.5^\circ \times \sin 22.5^\circ ) $
For 8 current-carrying cables, the total magnetic field will be8 times the magnetic field due to one current-carrying cable
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi a}}(32 \times \tan 22.5^\circ \times \sin 22.5^\circ ) $
Which can then be simplified to,
$\Rightarrow B = \dfrac{{5{\mu _0}I}}{{4\pi a}} $ which corresponds to option (A).

Note
We can alternatively find the magnetic field using the formula for a polygon of $ n $ sides that has perimeter $ P $ as:
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi P}}4{n^2}\tan \left( {\dfrac{\pi }{n}} \right)\sin \left( {\dfrac{\pi }{n}} \right) $
Since $ P = 8a $ and $ n = 8 $ , we can determine
 $\Rightarrow B = \dfrac{{{\mu _0}I}}{{4\pi a}}(32 \times \tan 22.5^\circ \times \sin 22.5^\circ ) $ which again gives us option (A).