Question

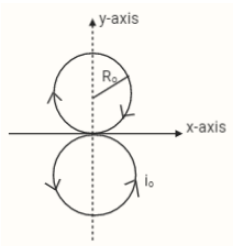
A current carrying wire frame is in the shape of digit eight $\left( 8 \right)$ . It is carrying current ${i_o}$ . If the radius of each loop is ${R_o}$ , then the net magnetic field dipole moment of the figure is

A. $\dfrac{{{i_o}\pi {R_o}^2}}{{\sqrt 2 }}$
B. $Zero$
C. ${i_o} \times 2\pi {R_o}^2$
D. ${i_o} \times \left( {4\pi {R_o}} \right)$

Answer 1

Hint: The magnetic dipole moment is the product of current flowing in a loop and area of cross-section of the loop. The net magnetic dipole moment is the sum of dipole moments in both the loops and the direction of current in the upper loop is opposite to the direction of current in the lower loop which is represented by the arrow mark.

Complete step by step solution:
A wire frame is in a shape of eight $\left( 8 \right)$ which carries current ${i_o}$ as shown in the above figure i.e., the current is flowing in a clockwise direction in the upper circle and it is flowing in an anticlockwise direction in the lower circle. The radius of each loop is ${R_o}$ .

We know that every current carrying loop is a magnetic dipole and has two poles- South and North. In the upper loop, the current is flowing in the south direction and in the lower circle it is flowing in the north direction. Magnetic field lines arise from the North Pole. Each magnetic dipole has some magnetic moment $\left( M \right)$ . The magnitude of $M$ is given by the formula $M = NIA$ where $N$ is the number of turns in a loop, I is the magnitude of current in the loop and A is the area of cross-section of the loop.

Let the magnetic dipole moment in the upper loop be ${M_1}$ and ${M_2}$ be the magnetic dipole moment in the lower loop. Hence, ${M_1} = N{i_o}\left( {A_1} \right)$ where ${A_1}$ is the area of the upper loop.

${M_1} = {i_o}\left( {\pi {R_o}^2} \right)$ [ since there is only one turn in the loop and area of a circle is ${\pi{r^2}}$.
and ${M_2} = N{i_o}\left( {A_2} \right)$ where ${A_2}$ is the area of the lower loop.
$M2 = {i_o}\left( {\pi {R_o}^2} \right)$ [ since radius is same in each loop]
The net magnetic dipole moment $\left( M \right) = {M_1} + {M_2}$
$M = {i_o}\left( {\pi {R_o}^2} \right) - {i_o}\left( {\pi {R_o}^2} \right)$ [since the direction of both the dipole magnetic moment is opposite to each other]
$\therefore M = 0$

Therefore, option B is correct.

Note:We should remember that the direction of magnetic dipole moment in both the loops is opposite to each other because the direction of magnetic dipole moment is North in the lower loop and South in the upper loop which can be denoted by the end points of letter N and S.