Question

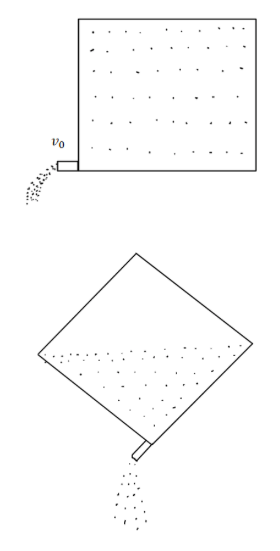
A cuboidal box of wine has a small spout located in one of the bottom corners. When the box is full and placed on a level surface, opening the spout results in a flow of wine with an initial speed of ${v_o}$(see figure). When the box is half empty, someone tilts it at ${45^\circ }$ so that the spout is at the lowest point (see figure). When the spout is opened the wine will flow out with a speed of

A) ${v_o}$.
B) $\dfrac{{{v_o}}}{2}$.
C) $\dfrac{{{v_o}}}{{\sqrt 2 }}$.
D) $\dfrac{{{v_o}}}{{\sqrt[4]{2}}}$

Answer 1

Hint:The concept and formula of Torricelli's law can be used to solve this problem and get the correct answer for this problem. According to Torricelli’s law the velocity of the fluid flowing out of any container is equal to the speed of a freely falling body.

Formula used:
The formula of Torricelli’s law can be given by $v = \sqrt {2gh} $ where $h$ is the height of the container till which the fluid is filled.

Complete step by step answer:
Let the height of the cuboidal be ‘$a$’ and as all the sides of the cuboidal is ‘$a$’ therefore the length of the diagonal is equal to ‘$\sqrt 2 \cdot a$’.
The velocity of the fluid is ${v_o} = \sqrt {2ga} $ where ‘a’ is the height of the box till which the wine is filled inside the box.
Now after half of the box of wine is empty then the height till which wine is filled is half of the diagonal therefore the vertical height is half of the diagonal. So the height $h = \dfrac{{\sqrt 2 \cdot a}}{2} = \dfrac{a}{{\sqrt 2 }}$
Applying the Torricelli’s law we get
$ \Rightarrow v = \sqrt {2gh} $
$ \Rightarrow v = \sqrt {2 \cdot g \cdot \dfrac{a}{{\sqrt 2 }}} $………(on comparing the equation with the initial velocity of the wine we get.)
$ \Rightarrow v = \dfrac{{{v_o}}}{{\sqrt[4]{2}}}$
So the correct answer for this problem is $v = \dfrac{{{v_o}}}{{\sqrt[4]{2}}}$which is option D.

Note:It is advisable for the students to understand and remember the concept of Torricelli’s law, also the formula involving the terms velocity and height till which the fluid is filled. The students should not get confuse in the step where the velocity of the wine from the corner is equal to the value of $v = \dfrac{{{v_o}}}{{\sqrt[4]{2}}}$ here we must see that the value of ${v_o} = \sqrt {2ga} $ where ‘a’ is the side of the cuboid and the velocity of the wine after half of the wine left the box is given by $v = \sqrt {2 \cdot g \cdot \dfrac{a}{{\sqrt 2 }}} $ so if we compare the this velocity with the initial velocity then we get the required answer.