Question

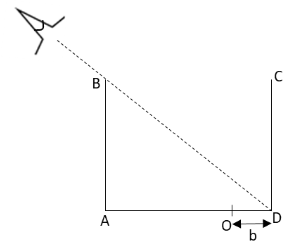
A cubical vessel with opaque walls is so placed that the eye of an observer cannot see its bottom but can see the entire wall CD. A small object is placed at O at a distance \[b = 10\,{\text{cm}}\] from corner D. What minimum depth of water (\[\mu = \dfrac{4}{3}\]) should be poured into the vessel which will enable the observer to see the object?

A. \[28.6\,{\text{cm}}\]
B. \[26.7\,{\text{cm}}\]
C. \[22.4\,{\text{cm}}\]
D. \[20\,{\text{cm}}\]

Answer 1

Hint:Use the expression for Snell’s law. Using this expression for Snell’s law, calculate the value of sine of angle of incidence of the ray from the object at point O in the vessel travelling from water medium to air medium toward the eye of the observer. Then by using the trigonometric ratio of tan of an angle calculate the value of tan of angle of incidence of the light ray travelling from water to air medium. Then calculate the height of the water level in the water upto which the water should be poured.

Formula used:
The expression for Snell’s law is
\[{\mu _1}\sin i = {\mu _2}\sin r\] …… (1)
Here, \[{\mu _1}\] and \[{\mu _2}\] are refractive indices of the two media, \[i\] is angle of incidence and \[r\] is angle of refraction.

Complete step by step answer:
We have given that the vessel ABCD is a cube and the observer can see the wall CD of the vessel but cannot see the object at point O. The distance between the points O and D is
\[b = 10\,{\text{cm}}\]
The refractive index of the water medium is \[\dfrac{4}{3}\].
\[{\mu _W} = \dfrac{4}{3}\]
We have asked to calculate the height upto which the vessel should be filled with water so that the observer can see the object at point O.

Let us redraw the given diagram as

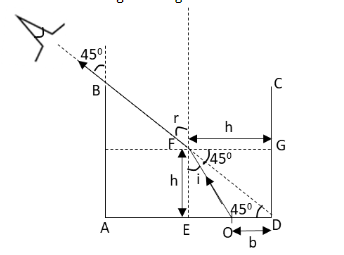
From the above diagram, we can write
\[{\text{FG}} = {\text{ED}} = h\] and
\[{\text{EO}} = h - b\]
Let us apply Snell law to the above system.
\[{\mu _W}\sin i = {\mu _A}\sin r\]
Here, \[{\mu _A}\] is a refractive index of air.
\[ \Rightarrow \sin i = \dfrac{{{\mu _A}\sin r}}{{{\mu _W}}}\]
\[ \Rightarrow \sin i = \dfrac{{\left( 1 \right)\sin 45^\circ }}{{\dfrac{4}{3}}}\]
\[ \Rightarrow \sin i = \dfrac{3}{{4\sqrt 2 }}\]

We can draw from this value

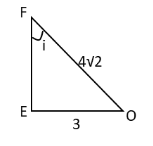
Hence,
\[ \Rightarrow \tan i = \dfrac{3}{{{\text{EF}}}}\]
\[ \Rightarrow \tan i = \dfrac{3}{{\sqrt {{{\left( {{\text{4}}\sqrt 2 } \right)}^2} - {3^2}} }}\]
\[ \Rightarrow \tan i = \dfrac{3}{{\sqrt {32 - 9} }}\]
\[ \Rightarrow \tan i = \dfrac{3}{{\sqrt {23} }}\]

We can also write
\[ \Rightarrow \tan i = \dfrac{{{\text{OE}}}}{{{\text{EF}}}}\]
\[ \Rightarrow \dfrac{3}{{\sqrt {23} }} = \dfrac{{h - b}}{h}\]
\[ \Rightarrow \dfrac{3}{{\sqrt {23} }} = 1 - \dfrac{b}{h}\]
\[ \Rightarrow \dfrac{b}{h} = 1 - \dfrac{3}{{\sqrt {23} }}\]
\[ \Rightarrow \dfrac{b}{h} = \dfrac{{\sqrt {23} - 3}}{{\sqrt {23} }}\]
\[ \Rightarrow \dfrac{b}{h} = \dfrac{{4.796 - 3}}{{4.796}}\]
\[ \Rightarrow \dfrac{b}{h} = \dfrac{{1.796}}{{4.796}}\]
\[ \Rightarrow h = \dfrac{{4.796b}}{{1.796}}\]
Substitute \[10\,{\text{cm}}\] for \[b\] in the above equation.
\[ \Rightarrow h = \dfrac{{4.796\left( {10\,{\text{cm}}} \right)}}{{1.796}}\]
\[ \therefore h = 26.7\,{\text{cm}}\]
Therefore, the height upto which the water should be poured in the vessel is \[26.7\,{\text{cm}}\].

Hence, the correct option is B.

Note:The students should be careful while using the trigonometric ratio for the angle of incidence of the light ray from the object at point O placed in the water. If we take these ratios incorrect then the values of all the next quantities we determine while performing further calculations will be incorrect. Hence, the final answer will also be incorrect.