Question

A cubical vessel of height 1m is full of water. What is the amount of work done in pumping water out of the vessel? (Take $g=10\text{ m/}{{\text{s}}^{2}}$)

A. 1250 J
B. 5000 J
C. 1000 J
D. 2500 J

Answer 1

Hint: Water contained inside a vessel can be considered to be a homogeneous object. Hence, we can assume that the centre of mass will be in the middle of the container. We can calculate the change in potential energy to determine the work done. Work done is equal to the negative of the change in potential energy.

Formula Used:
Potential energy of an object at a given height is,
U=mgh

Where,
m is the mass of the object
g is the gravitational acceleration
h is the height from the surface

Complete step by step answer:
Let us look at the following diagram to understand the initial condition of the system:

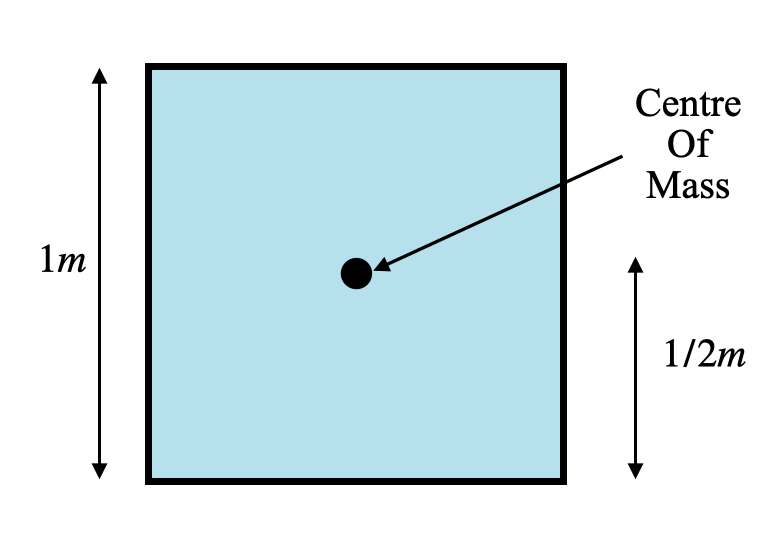
The diagram shows the position of the centre of mass of the water, which is at a height of ½ m from the ground.

First, let us calculate the mass of the water inside the cubical vessel.
It is given that the height of the cubical vessel is 1m

So, the volume of the vessel is
$1\text{ }{{\text{m}}^{3}}={{10}^{3}}\text{ L}$

The density of water can be assumed to be 1 kg/L.
Hence the mass of the water is,
${{10}^{3}}\text{ kg}$
Potential energy is given by,
U=mgh
Initially, the mass of water,
$\text{m}={{10}^{3}}\text{ kg}$
The height of the water can be considered to be at the centre of mass.
Hence, the height is given by,
$h=\dfrac{1}{2}\text{ m}$
Gravitational acceleration is given by,
$g=10\text{ m/}{{\text{s}}^{2}}$
So, the initial potential energy is,
${{U}_{i}}=\left( {{10}^{3}} \right)(10)\left( \dfrac{1}{2} \right)=5000\text{ J}$
We can assume that the water is kept at ground level after pumping out.

Hence, the height will be 0.

So, the final potential energy is,
${{U}_{f}}=0$

Work done is equal to the negative of the change in potential energy.

Hence, we can write,
$W=-\Delta U$
$\Rightarrow W=-({{U}_{f}}-{{U}_{i}})$
$\Rightarrow W=-\left( 0-5000 \right)$
$\Rightarrow W=5000$

So, work done is 5000 J.
The correct option is (B).

Note:
Positive work suggests that we are working against the force of gravitation. Although we are bringing the water to a lower potential, the work is positive. We can take an example of a ball dropping from a certain height. If we leave the ball, it will gain some kinetic energy in the process. We are restricting in gain in the kinetic energy in our case, that is the work done is positive.