Question

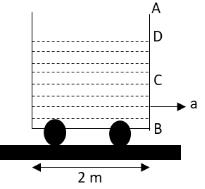
A cubical container (open from top) with side \[2\,{\text{m}}\] has a small hole with a cap at point C as shown. The water level is upto point D. (\[{\text{BC}} = 0.5\,{\text{m}}\] and \[{\text{BD}} = 5.5\,{\text{m}}\]). If container is given an acceleration of \[8\,{\text{m/}}{{\text{s}}^2}\] and the hole is opened simultaneously, the amount of water that spill out of the container is \[\left( {400 + x \times 100} \right)\,{\text{litres}}\]. Calculate \[x\].

A.7
B.5
C.3
D.8

Answer 1

Hint: First we should calculate the initial volume of water in the container. Then draw the diagram of the water container when the container starts moving (with the upper surface of the water tilted) and calculate the dimensions of the container upto which the water is filled. Calculate the volume of the water after the container starts moving using changed dimensions of the water in the container. Calculate the water spilled out of the container and equate it with the given volume of spilled water. Hence, determine the value of x.

Formula used:
The volume \[V\] of a cube is given by
\[V = {L^3}\]
Here, \[L\] is the length of the side of the cube.

Complete step by step answer:
We have given that the length of each side of the cubical container is \[2\,{\text{m}}\].
\[L = 2\,{\text{m}}\]. We have also given that \[{\text{BC}} = 0.5\,{\text{m}}\] and \[{\text{BD}} = 5.5\,{\text{m}}\].
The acceleration of the container is \[8\,{\text{m/}}{{\text{s}}^2}\].
\[a = 8\,{\text{m/}}{{\text{s}}^2}\]
Let us first calculate the initial volume \[{V_i}\] of the water in the cubical container.
\[{V_i} = \left( {2\,{\text{m}}} \right)\left( {2\,{\text{m}}} \right) \times {\text{BD}}\]
\[ \Rightarrow {V_i} = \left( {2\,{\text{m}}} \right)\left( {2\,{\text{m}}} \right) \times \left( {1.5\,{\text{m}}} \right)\]
\[ \Rightarrow {V_i} = 6\,{{\text{m}}^3}\]
\[ \Rightarrow {V_i} = \left( {6\,{{\text{m}}^3}} \right)\left( {\dfrac{{{{10}^3}\,{\text{litre}}}}{{1\,{{\text{m}}^3}}}} \right)\]
\[ \Rightarrow {V_i} = 6000\,{\text{litre}}\]
Hence, the volume of the water in the container before the container starts moving is \[6000\,{\text{litre}}\].

When the container starts moving, the upper surface of the water in the container gets tilted as shown in the below diagram.

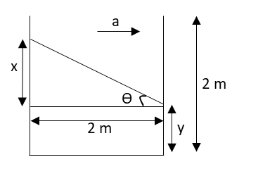
Now we need to determine the values of x and y. From the above diagram, we can write
\[\tan \theta = \dfrac{a}{g}\]
\[ \Rightarrow \tan \theta = \dfrac{{8\,{\text{m/}}{{\text{s}}^2}}}{{10\,{\text{m/}}{{\text{s}}^2}}}\]
\[ \Rightarrow \tan \theta = 0.8\]
We can also write from the above diagram that
\[\tan \theta = \dfrac{x}{{2\,{\text{m}}}}\]
\[ \Rightarrow 0.8 = \dfrac{x}{{2\,{\text{m}}}}\]
\[ \Rightarrow x = 1.6\,{\text{m}}\]
We can write that
\[ \Rightarrow x + y = 2\,{\text{m}}\]
\[ \Rightarrow y = 2\,{\text{m}} - x\]
\[ \Rightarrow y = 2\,{\text{m}} - 1.6\,{\text{m}}\]
\[ \Rightarrow y = 0.4\,{\text{m}}\]
Hence, the volume \[{V_f}\] of the water in the container after the container starts moving is given by
\[{V_f} = \left[ {\dfrac{{\left( {x + y} \right) + y}}{2}} \right]\left( {2\,{\text{m}}} \right)\left( {2\,{\text{m}}} \right)\]
\[ \Rightarrow {V_f} = \left[ {\dfrac{{\left( {1.6\,{\text{m}} + 0.4\,{\text{m}}} \right) + \left( {0.4\,{\text{m}}} \right)}}{2}} \right]\left( {2\,{\text{m}}} \right)\left( {2\,{\text{m}}} \right)\]
\[ \Rightarrow {V_f} = 4.8\,{{\text{m}}^3}\]
\[ \Rightarrow {V_f} = 4800\,{\text{litre}}\]
Hence, the volume of the water when the container starts moving is \[4800\,{\text{litre}}\].

Let us now calculate the volume \[V\] of the water that spills out of the container.
\[V = {V_i} - {V_f}\]
Substitute \[6000\,{\text{litre}}\] for \[{V_i}\] and \[4800\,{\text{litre}}\] for \[{V_f}\] in the above equation.
\[V = \left( {6000\,{\text{litre}}} \right) - \left( {4800\,{\text{litre}}} \right)\]
\[ \Rightarrow V = 1200\,{\text{litre}}\]
We have given that the volume of the water that spills out of the container is \[\left( {400 + x \times 100} \right)\,{\text{litres}}\].
Hence, we can write
\[\left( {400 + x \times 100} \right)\,{\text{litres}} = 1200\,{\text{litre}}\]
\[ \Rightarrow 100x\, = 1200 - 400\]
\[ \Rightarrow 100x\, = 800\]
\[ \therefore x = 8\]
Therefore, the value of x is 8.

Hence, the correct option is D.

Note: The students should not forget to convert the volume of the water in the container before and after the container starts moving in the unit litre as the given volume of the water that spills out of the water is in litre. Also the students should not get confused about how we have calculated the final volume of the water in the container. We have taken the average of the dimensions of the container up to which the water is filled and used the formula for volume of the cube.