Question

A cubical box has each edge equal to 10 cm and a cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(a) Which box has the greater lateral surface area and by how much?
(b) Which box has the smaller total surface area and by how much?

Answer 1

Hint: We know that the lateral surface area of a cube or cuboid is the area which excludes the top and bottom surface of the cube or cuboid. For cuboid, let us assume that length, breadth and height of the cube is l, b and h then the lateral surface area is equal to $2h\left( l+b \right)$ and let us assume that side of the cube is “a” so the lateral surface area of the cube is equal to $4{{a}^{2}}$. Now, substitute the values of the edge of the cube and length, breadth and height of the cuboid in the lateral surface area of the cube and cuboid and then compare. The total surface area of the cube and the cuboid is equal to $2\left( lb+bh+hl \right)$ and $6{{a}^{2}}$ respectively. Now, substitute the values of l, b , h and a in the above formula for total surface areas and then compare the total surface areas.

Complete step-by-step answer:
It is given that the edge length of the cube is 10 cm and length, breadth and height of the cuboid is given as 12.5 cm, 10 cm and 8 cm respectively.
The diagram of a cubical box of length 10 cm is shown below:

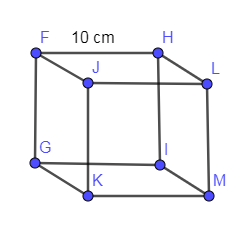
Let us assume that each edge length of the cube is “a”.
We know that lateral surface area of the cube is equal to:
$4{{a}^{2}}$
Substitute the value of “a” as 10 cm in the above expression we get,
$\begin{align}
  & 4{{\left( 10 \right)}^{2}} \\
 & =400c{{m}^{2}} \\
\end{align}$
We know that total surface area of the cube is equal to:
$6{{a}^{2}}$
Substituting the value of “a” as 10 cm in the above expression we get,
$\begin{align}
  & 6{{\left( 10 \right)}^{2}} \\
 & =600c{{m}^{2}} \\
\end{align}$
From the above calculations, we have found the lateral surface area of the cubical box as $400c{{m}^{2}}$ and total surface area of the cubical box is $600c{{m}^{2}}$.
In the below diagram, we have drawn a cuboidal box of length, breadth and height as 12.5 cm, 10 cm and 8 cm respectively.

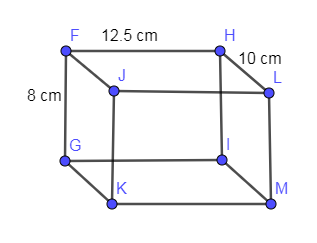
In the above diagram, we have shown the length of cuboid as FH, breadth as HL and height as FG.
Let us assume that length, breadth and height of the cuboid is l, b and h respectively.
We know that lateral surface area of the cuboid is equal to:
$2h\left( l+b \right)$
Substituting the value of l as 12.5 cm, b as 10 cm and h as 8 cm in the above expression we get,
$\begin{align}
  & 2\left( 8 \right)\left( 12.5+10 \right) \\
 & =16\left( 22.5 \right) \\
 & =360c{{m}^{2}} \\
\end{align}$
We know that total surface area of the cuboid is equal to:
$2\left( lb+bh+hl \right)$
Substituting the value of l, b and h as we have calculated above in the above expression we get,
$\begin{align}
  & 2\left( 12.5\left( 10 \right)+10\left( 8 \right)+8\left( 12.5 \right) \right) \\
 & =2\left( 125+80+100 \right) \\
 & =2\left( 305 \right) \\
 & =710c{{m}^{2}} \\
\end{align}$
Hence, the total surface area of the cuboidal box is equal to $710c{{m}^{2}}$ and lateral surface area of the cuboidal box is equal to $360c{{m}^{2}}$.
Now, using the above information we are going to solve the two parts given in the question.
In part (a), we have to determine which box has greater lateral surface area.
The lateral surface area of cubical box is equal to $400c{{m}^{2}}$ whereas the lateral surface area of cuboidal box is equal to $360c{{m}^{2}}$. A
From the above, you can see that the lateral surface area of the cubical box is greater than the cuboidal box.
The difference of the lateral surface areas of the two boxes will give us how much the cubical box is greater than the cuboidal box.
$\begin{align}
  & \left( 400-360 \right)c{{m}^{2}} \\
 & =40c{{m}^{2}} \\
\end{align}$
Hence, the lateral surface area of the cubical box is greater than the cuboidal box by $40c{{m}^{2}}$.
In part (b), we have to determine which box has a smaller total surface area.
In the above, we have obtained the total surface area of the cubical box as $600c{{m}^{2}}$ and the total surface area of the cuboidal box as $710c{{m}^{2}}$.
This shows that the total surface area of the cubical box is greater than the cubical box. The difference of the two boxes total surface area is given as:
$\begin{align}
 & \left( 710-600 \right)c{{m}^{2}} \\
 & =110c{{m}^{2}} \\
\end{align}$
Hence, the total surface area of the cuboidal box is greater than cubical box by $110c{{m}^{2}}$.

Note: The take home message from doing this problem is that the difference between lateral surface area and total surface area is that in the lateral surface area of the cube or cuboid we exclude the top and bottom surfaces of the cube or cuboid whereas in total surface area the top and bottom surfaces are included.
Let us take the example of a cube with an edge length of 10 cm that we have solved above.
The lateral surface area of the cube is $400c{{m}^{2}}$ whereas the total surface area is $600c{{m}^{2}}$.
The area of top and bottom surface of cube is $100c{{m}^{2}}$ and $100c{{m}^{2}}$ respectively so while calculating the total surface area we have included the areas of both top and bottom surfaces.
The sum of surface areas of top and bottom is equal to $200c{{m}^{2}}$ so when we add $200c{{m}^{2}}$ in the lateral surface area which is $\left( 400c{{m}^{2}} \right)$ we get $600c{{m}^{2}}$ and $600c{{m}^{2}}$ is the total surface area of the cubical box.