Question

A cubical box has each edge $10\text{ }cm$ and another cubical box is $12.5\text{ }cm$long, $10\text{ }cm$ wide and $\text{8 }cm$ high. Which box has the smaller total surface area (in sq.cm) and by how much?

Answer 1

Hint: Here two cubical boxes are given. We have to find the total surface area of the two cubical boxes with one box of side $10\text{ }cm$ and other box with length, $l=12.5\text{ }cm$, breadth $b=10\text{ }cm$ and height, $h=8\text{ }cm$.First box is a cube, and the other is a cuboid. We can find the total surface area by the two formulas:

Complete Step-by-step answer:
Total surface area of the cube $=6{{a}^{2}}$
Total surface area of the cuboid $=2\left( lb+bh+lh \right)$

Here, we are given with two boxes.
Now, we have to calculate the total surface areas of two boxes to find which has the smaller total surface area.
We are given that the first box has each edge of length $a=10\text{ }cm$. Therefore we can say that the first box is a cube, since all sides are equal.
For the first box consider the figure:

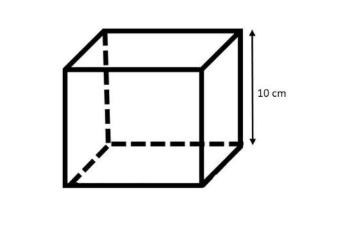
Now, we have to calculate the total surface area $(TSA)$ of the cube. It is given by the formula:
$\begin{align}
  & TSA=6{{a}^{2}} \\
 & TSA=6\times {{10}^{2}} \\
 & TSA=6\times 100 \\
 & TSA=600 \\
\end{align}$
Hence, the total surface area of the cube is $600\text{ }c{{m}^{2}}$.
Next, consider the second box of length $l=12.5\text{ }cm$, breadth $b=10\text{ }cm$ and height $h=10\text{ }cm$. Therefore we can say that the second box is a cuboid.
Since, the second box is a cuboid, we have the figure:

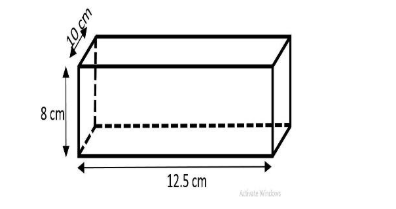
Now, we have to calculate the total surface area $(TSA)$ of the cuboid. It is given as:
$\begin{align}
  & TSA=2\left( lb+bh+lh \right) \\
 & TSA=2(12.5\times 10+10\times 8+12.5\times 8) \\
 & TSA=2(125+80+100) \\
 & TSA=2\times 305 \\
 & TSA=610 \\
\end{align}$
Hence the total surface area of the cuboid is $610\text{ }c{{m}^{2}}$
TSA of the cube - TSA of the cuboid $=610-600=10\text{ }c{{m}^{2}}$
Therefore, we can say that the total surface area of the first box is $10\text{ }c{{m}^{2}}$ smaller than the second box.

Note: Here, the first box is a cube, since all sides of a cube are of equal length. So you have to calculate the total surface area of the cube. The second box is a cuboid, therefore we have to calculate the total surface area of the cuboid. After getting the area don’t forget to calculate the difference in area which is the required answer.